Is 5 8 Smaller Than 1 2
Kalali
Jul 15, 2025 · 5 min read
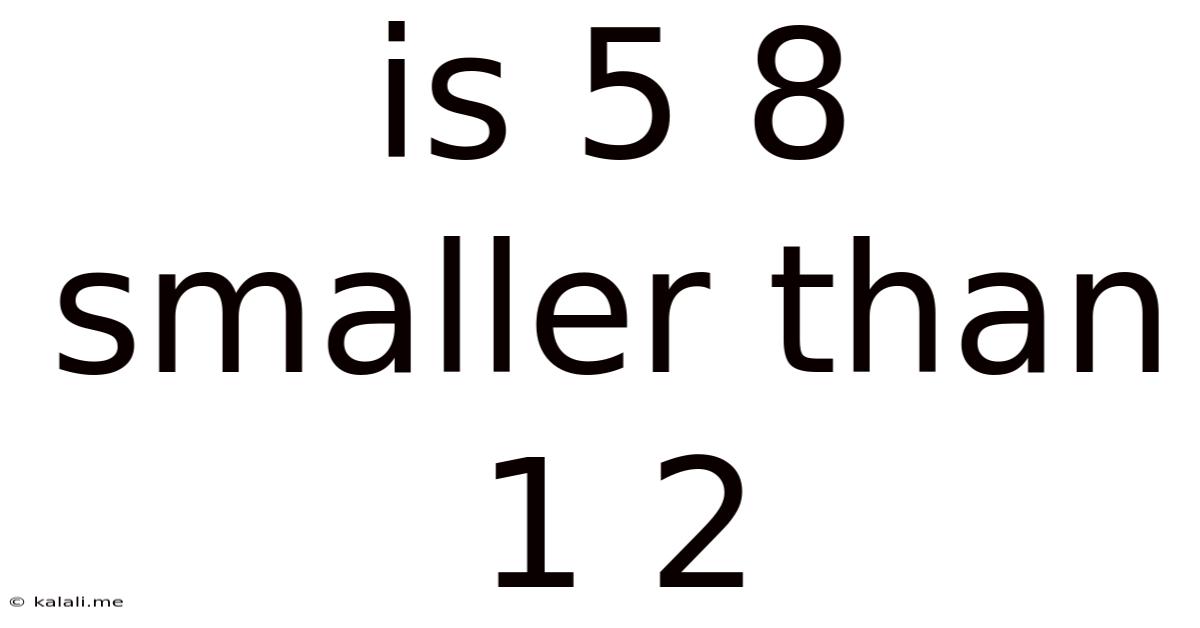
Table of Contents
Is 5/8 Smaller Than 1/2? A Deep Dive into Fraction Comparison
This article will comprehensively explore the question: "Is 5/8 smaller than 1/2?" We'll delve into various methods for comparing fractions, explaining the concepts clearly and providing practical examples. This will not only answer the initial question but also equip you with the skills to compare any two fractions effectively. Understanding fraction comparison is fundamental to mathematics and crucial for various applications in everyday life and advanced studies.
Understanding Fractions
Before we tackle the comparison, let's briefly refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 5/8, 5 is the numerator and 8 is the denominator. This means we have 5 out of 8 equal parts.
Method 1: Finding a Common Denominator
This is a classic and reliable method for comparing fractions. The core principle is to convert both fractions to equivalent fractions with the same denominator. This allows for a direct comparison of the numerators.
To find a common denominator for 5/8 and 1/2, we need to find a number that is a multiple of both 8 and 2. The least common multiple (LCM) is often the most efficient choice. In this case, the LCM of 8 and 2 is 8.
- Converting 1/2: To change the denominator of 1/2 to 8, we multiply both the numerator and denominator by 4 (because 2 x 4 = 8). This gives us 4/8.
Now we can compare:
- 5/8 and 4/8
Since 5 > 4, we conclude that 5/8 is greater than 4/8, and therefore, 5/8 is greater than 1/2.
Method 2: Converting to Decimals
Another effective method is to convert both fractions into decimal numbers. This allows for a straightforward comparison using the decimal number line.
-
Converting 5/8: Divide the numerator (5) by the denominator (8): 5 ÷ 8 = 0.625
-
Converting 1/2: Divide the numerator (1) by the denominator (2): 1 ÷ 2 = 0.5
Now we compare the decimal values: 0.625 and 0.5.
Since 0.625 > 0.5, we confirm that 5/8 is greater than 1/2.
Method 3: Visual Representation
Visual aids can be particularly helpful for understanding fraction comparison, especially for beginners. Imagine a circle divided into 8 equal parts. Shading 5 of these parts represents 5/8. Now, imagine another circle divided into 2 equal parts. Shading 1 part represents 1/2.
Visually comparing the shaded areas clearly shows that the shaded area representing 5/8 is larger than the shaded area representing 1/2. This provides a concrete understanding of the comparison.
Method 4: Using a Number Line
A number line provides a visual representation of the relative positions of numbers. Plotting both fractions on a number line helps visualize their relative sizes.
You'll find that 5/8 is positioned to the right of 1/2, indicating that 5/8 is greater than 1/2.
Beyond the Basic Comparison: Understanding Fraction Relationships
While answering the primary question is straightforward, let's expand our understanding by exploring related concepts and scenarios.
1. Equivalent Fractions: Remember that fractions can be equivalent even if they look different. For example, 1/2, 2/4, 4/8, and 8/16 are all equivalent fractions because they represent the same proportion of a whole. Understanding equivalent fractions is crucial for simplifying fractions and comparing them effectively.
2. Improper Fractions and Mixed Numbers: An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 7/4). A mixed number combines a whole number and a fraction (e.g., 1 ¾). Converting between improper fractions and mixed numbers is a skill needed for various fraction operations, including comparison.
3. Comparing More Than Two Fractions: The methods discussed above can be extended to compare more than two fractions. Finding a common denominator remains the most reliable method for accurate comparison. Consider the fractions 1/3, 2/5, and 3/8. Finding a common denominator (e.g., 120) allows for a direct comparison of their numerators.
4. Applications of Fraction Comparison:
Fraction comparison isn't just an academic exercise. It has practical applications in many areas, including:
- Cooking and Baking: Following recipes often requires understanding and comparing fractions of ingredients.
- Construction and Engineering: Precise measurements and calculations often involve fraction comparison.
- Finance and Budgeting: Managing finances requires understanding and comparing fractions of income and expenses.
- Data Analysis: Data interpretation frequently involves comparing fractions and proportions.
Practical Exercises:
To solidify your understanding, try comparing the following fractions using the methods described above:
- 3/4 and 2/3
- 7/10 and 3/5
- 5/6 and 7/8
- 2/9 and 1/5
- 11/12 and 9/10
By practicing these exercises, you will strengthen your ability to compare fractions accurately and confidently. Remember, the key is to find a method that works best for you, whether it's finding a common denominator, converting to decimals, using visual aids, or employing a number line.
Conclusion:
We've definitively answered the question: 5/8 is not smaller than 1/2; it is larger. Furthermore, we’ve explored several methods for comparing fractions, emphasizing the importance of understanding these techniques for solving a wide range of mathematical problems and applying this knowledge to real-world situations. Mastering fraction comparison is a valuable skill that will serve you well in various aspects of life. Remember to practice regularly to build your confidence and proficiency.
Latest Posts
Latest Posts
-
How Many Tenths Are In An Inch
Jul 15, 2025
-
Which Word Has The Most Positive Connotation
Jul 15, 2025
-
How Do I Send An Evite Reminder
Jul 15, 2025
-
When Performing A Self Rescue When Should You Swim To Shore
Jul 15, 2025
-
How Many Decaliters Are In A Liter
Jul 15, 2025
Related Post
Thank you for visiting our website which covers about Is 5 8 Smaller Than 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.