Is 7 8 Bigger Than 3 4
Kalali
Jul 03, 2025 · 5 min read
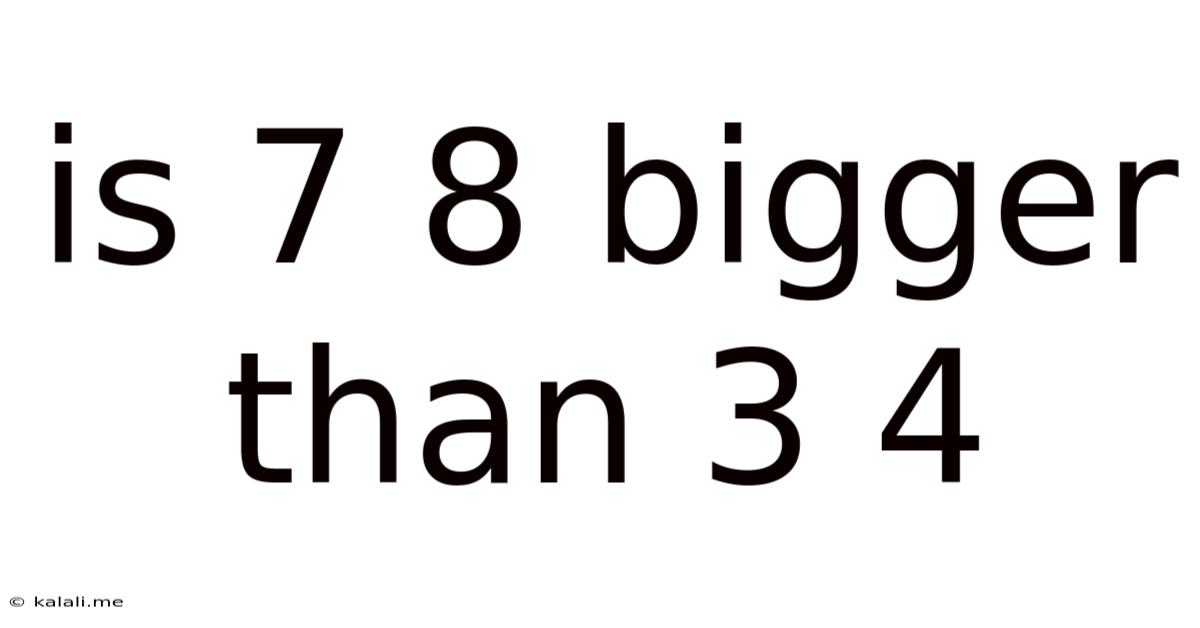
Table of Contents
Is 7/8 Bigger Than 3/4? A Deep Dive into Fraction Comparison
This seemingly simple question, "Is 7/8 bigger than 3/4?", opens the door to a broader understanding of fractions, a fundamental concept in mathematics with far-reaching applications in everyday life. While the answer itself is straightforward, exploring the various methods to compare fractions offers valuable insights into numerical reasoning and problem-solving skills. This article delves into multiple approaches to determine the relative sizes of 7/8 and 3/4, providing a comprehensive guide suitable for students and adults alike. We'll explore visual representations, equivalent fractions, decimal conversions, and cross-multiplication, reinforcing the understanding of fractional comparisons.
Understanding Fractions: A Quick Recap
Before jumping into the comparison, let's briefly review the components of a fraction. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of equal parts the whole is divided into. For instance, in the fraction 7/8, 7 is the numerator and 8 is the denominator. This means we have 7 out of 8 equal parts.
Method 1: Visual Representation
A simple and intuitive way to compare fractions is through visual representation. Imagine two identical circles. Divide the first circle into 8 equal slices and shade 7 of them (representing 7/8). Divide the second circle into 4 equal slices and shade 3 of them (representing 3/4). By visually comparing the shaded areas, it becomes clear that the shaded area representing 7/8 is larger than the shaded area representing 3/4. This method is particularly helpful for beginners as it provides a concrete, easily understandable comparison.
Method 2: Finding Equivalent Fractions
Another effective method involves finding equivalent fractions. Equivalent fractions represent the same value but have different numerators and denominators. To compare 7/8 and 3/4, we need to find a common denominator. The least common multiple (LCM) of 8 and 4 is 8.
We can convert 3/4 to an equivalent fraction with a denominator of 8 by multiplying both the numerator and the denominator by 2:
(3/4) x (2/2) = 6/8
Now we can easily compare 7/8 and 6/8. Since 7 > 6, we can conclude that 7/8 is greater than 6/8, and therefore, 7/8 is greater than 3/4. This method emphasizes the concept of equivalent fractions and provides a systematic approach to fraction comparison.
Method 3: Converting to Decimals
Converting fractions to decimals offers another way to compare their values. To convert a fraction to a decimal, divide the numerator by the denominator.
7/8 = 0.875
3/4 = 0.75
By comparing the decimal values, it's evident that 0.875 is greater than 0.75, confirming that 7/8 is larger than 3/4. This method is particularly useful when dealing with fractions that are difficult to visualize or find equivalent fractions for. Understanding decimal representation is crucial for various mathematical operations and real-world applications.
Method 4: Cross-Multiplication
Cross-multiplication provides a more algebraic approach to comparing fractions. To compare fractions a/b and c/d, we cross-multiply:
- a x d and b x c
If a x d > b x c, then a/b > c/d.
Let's apply this to 7/8 and 3/4:
- 7 x 4 = 28
- 8 x 3 = 24
Since 28 > 24, we conclude that 7/8 > 3/4. This method is efficient and mathematically rigorous, providing a solid foundation for understanding fraction comparison.
Beyond the Comparison: Real-World Applications
The ability to compare fractions is not just an abstract mathematical skill; it has numerous practical applications in daily life. Consider these examples:
- Baking: Recipes often require precise measurements using fractions. Understanding fraction comparison ensures you use the correct amount of ingredients.
- Construction: Accurate measurements are critical in construction, and the ability to compare fractions helps ensure the precision needed for projects.
- Finance: Calculating percentages, interest rates, and portions of investments all involve working with fractions and their comparisons.
- Data Analysis: Interpreting data often involves understanding fractions and proportions, requiring the skill of comparing fractional values.
Expanding the Knowledge: Working with Improper and Mixed Fractions
While the example focuses on proper fractions (where the numerator is smaller than the denominator), the same principles apply to improper fractions (where the numerator is larger than or equal to the denominator) and mixed fractions (a combination of a whole number and a proper fraction).
For example, compare 5/4 and 1 1/2. First convert both to improper fractions: 5/4 and 3/2. Then, use any of the methods described above (e.g., find a common denominator or cross-multiply) to determine which is larger. 5/4 (1.25) is smaller than 3/2 (1.5).
Conclusion: Mastering Fraction Comparison
Determining whether 7/8 is bigger than 3/4 is a fundamental exercise that highlights the importance of understanding fraction comparison. This seemingly simple question opens doors to various methods, each providing a unique perspective and reinforcing the underlying concepts. From visual representations to algebraic approaches, mastering these methods builds a strong foundation for tackling more complex mathematical problems and real-world applications. The ability to compare fractions is a crucial skill applicable across numerous fields, emphasizing its importance in both academic and practical contexts. Continuously practicing these methods will enhance mathematical proficiency and problem-solving abilities. Remember, understanding the "why" behind the calculations is just as important as obtaining the correct answer. This thorough exploration empowers learners to confidently navigate the world of fractions and their diverse applications.
Latest Posts
Latest Posts
-
How Do You Say Flour In Spanish
Jul 30, 2025
-
How Many Cups Of Soda In A 2 Liter Bottle
Jul 30, 2025
-
How Much Is A Half A Gallon Of Water
Jul 30, 2025
-
How Many Laps Is 300 Yards In A Pool
Jul 30, 2025
-
Only Letter Not In A State Name
Jul 30, 2025
Related Post
Thank you for visiting our website which covers about Is 7 8 Bigger Than 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.