Is 7 8 Greater Than 3 4
Kalali
Jul 16, 2025 · 5 min read
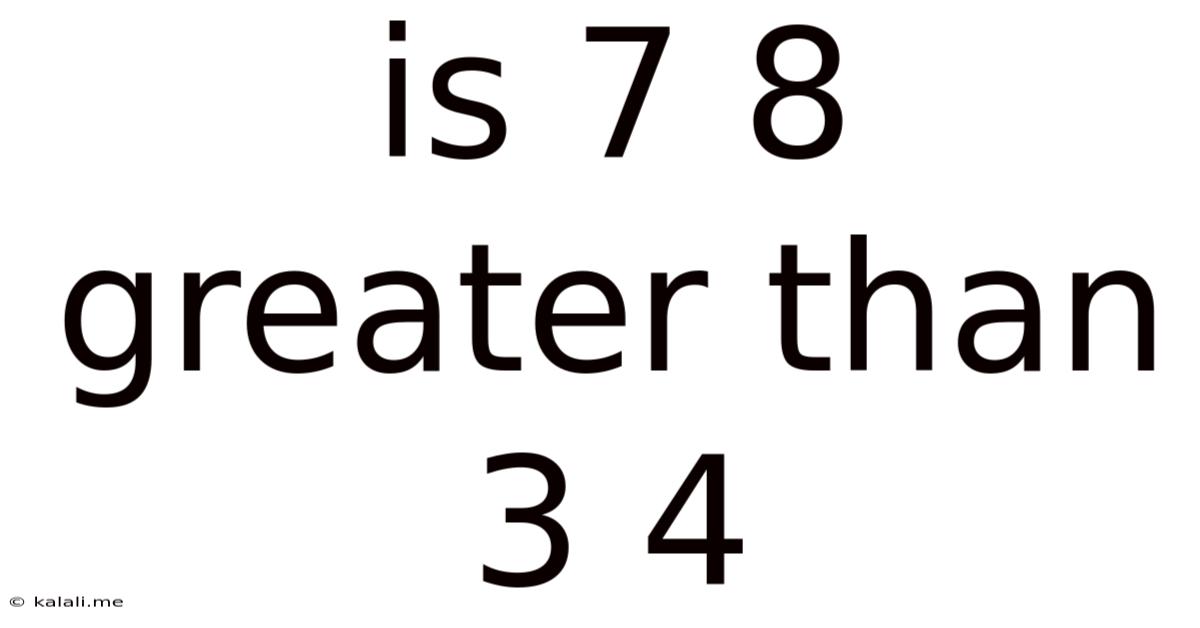
Table of Contents
Is 7/8 Greater Than 3/4? A Comprehensive Exploration of Fraction Comparison
This article delves into the seemingly simple question: Is 7/8 greater than 3/4? While the answer might appear obvious to some, a thorough understanding of fraction comparison is crucial for various mathematical applications and problem-solving scenarios. We'll not only answer the question definitively but also explore multiple methods for comparing fractions, providing a robust foundation for anyone working with fractions. This includes practical examples and tips to build confidence and skill in this fundamental area of mathematics.
Meta Description: Learn how to compare fractions effectively! This comprehensive guide explains multiple methods to determine if 7/8 is greater than 3/4, providing practical examples and strengthening your understanding of fraction comparison.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's briefly revisit the concept of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
For instance, in the fraction 7/8, the denominator 8 means the whole is divided into 8 equal parts, and the numerator 7 signifies that we're considering 7 of those parts.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. This involves converting both fractions so they share the same denominator. Once they have the same denominator, we can simply compare the numerators. The fraction with the larger numerator is the larger fraction.
Let's apply this to our problem: Is 7/8 greater than 3/4?
-
Find the least common multiple (LCM) of the denominators: The denominators are 8 and 4. The LCM of 8 and 4 is 8.
-
Convert the fractions to equivalent fractions with the common denominator:
- 7/8 already has a denominator of 8, so it remains 7/8.
- To convert 3/4 to an equivalent fraction with a denominator of 8, we multiply both the numerator and the denominator by 2: (3 x 2) / (4 x 2) = 6/8.
-
Compare the numerators: Now we compare 7/8 and 6/8. Since 7 > 6, we conclude that 7/8 > 6/8.
Therefore, 7/8 is greater than 3/4.
Method 2: Converting to Decimals
Another effective way to compare fractions is by converting them into decimals. This method is particularly useful when dealing with fractions that are difficult to compare using common denominators.
-
Convert each fraction to a decimal:
- 7/8 = 0.875
- 3/4 = 0.75
-
Compare the decimals: Since 0.875 > 0.75, we conclude that 7/8 > 3/4.
This method confirms our previous finding: 7/8 is greater than 3/4.
Method 3: Visual Representation
For a more intuitive understanding, especially for beginners, visualizing the fractions can be helpful. Imagine two identical circles.
-
Represent 7/8: Divide one circle into 8 equal slices and shade 7 of them.
-
Represent 3/4: Divide the second circle into 4 equal slices and shade 3 of them.
By visually comparing the shaded areas, it becomes clear that the area representing 7/8 is larger than the area representing 3/4. This visual confirmation reinforces the conclusion that 7/8 is greater than 3/4.
Addressing Potential Confusion and Common Mistakes
While comparing fractions might seem straightforward, some common pitfalls can lead to errors. Let's address some of these:
-
Incorrectly comparing numerators without considering denominators: Simply comparing the numerators (7 and 3) without accounting for the different denominators will lead to an incorrect conclusion. Remember, the denominator plays a vital role in determining the fraction's value.
-
Errors in finding the LCM or converting to equivalent fractions: Careless mistakes in calculating the least common multiple or converting fractions can result in inaccurate comparisons. Double-check your calculations to ensure accuracy.
-
Misinterpreting decimal representations: While decimal conversion is helpful, rounding errors can sometimes lead to slight inaccuracies. It’s best to use enough decimal places for a precise comparison.
Expanding the Concept: Comparing More Than Two Fractions
The methods discussed above can be extended to compare more than two fractions. For example, let's compare 7/8, 3/4, and 5/6.
-
Find the LCM of the denominators (8, 4, and 6): The LCM is 24.
-
Convert all fractions to equivalent fractions with a denominator of 24:
- 7/8 = 21/24
- 3/4 = 18/24
- 5/6 = 20/24
-
Compare the numerators: 21 > 20 > 18. Therefore, 7/8 > 5/6 > 3/4.
Practical Applications of Fraction Comparison
The ability to compare fractions is essential in various real-world situations and academic contexts:
-
Baking and Cooking: Following recipes often requires understanding and comparing fractional measurements of ingredients.
-
Construction and Engineering: Precise measurements and calculations in construction and engineering frequently involve fractions.
-
Data Analysis: Interpreting data represented as fractions or percentages necessitates comparing fractional values.
-
Financial Calculations: Understanding financial ratios and proportions requires proficiency in fraction comparison.
-
Everyday problem-solving: Many everyday problems, from dividing resources to understanding proportions, require the ability to compare fractions.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental skill in mathematics with broad applications. By understanding and mastering the methods discussed – finding a common denominator, converting to decimals, and visual representation – you'll develop confidence and accuracy in handling fractions. Remember to always double-check your work and choose the method that best suits the specific problem you are tackling. With practice, comparing fractions will become second nature, empowering you to tackle more complex mathematical challenges. The simple answer to the initial question, "Is 7/8 greater than 3/4?", is a resounding yes, but the journey to understanding why is what truly strengthens your mathematical abilities.
Latest Posts
Latest Posts
-
How Many Feet Is 100 Square Meters
Jul 16, 2025
-
What Is A Quarter Of An Ounce
Jul 16, 2025
-
How To Complete Level 12 On Bloxorz
Jul 16, 2025
-
Difference In Time Between California And Hawaii
Jul 16, 2025
-
How Many Sugar Cubes In A Cup Of Sugar
Jul 16, 2025
Related Post
Thank you for visiting our website which covers about Is 7 8 Greater Than 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.