Is 75 The Same As 3 4
Kalali
Jul 16, 2025 · 5 min read
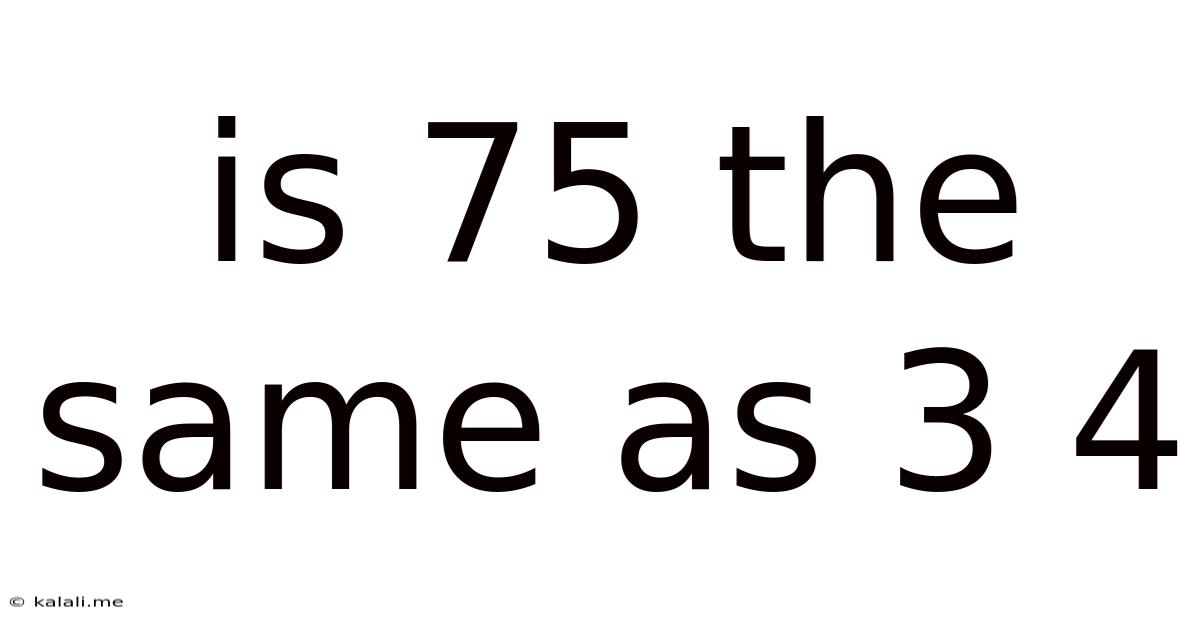
Table of Contents
Is 75 the Same as 3/4? Understanding Fractions and Decimals
This seemingly simple question, "Is 75 the same as 3/4?", delves into the fundamental concepts of fractions, decimals, and percentage equivalence. While a quick glance might suggest they are unrelated, understanding their interconnectedness is crucial for various mathematical applications and real-world scenarios. This article will explore the relationship between 75 (implicitly representing 75%), 3/4, and their equivalent representations, offering a comprehensive guide for both beginners and those looking to solidify their understanding of these core mathematical concepts.
Meta Description: This article explores the equivalence of 75 (75%), 3/4, and their various representations, explaining the conversion process between fractions, decimals, and percentages. Learn how to understand and apply these fundamental mathematical concepts.
Understanding Fractions
A fraction represents a part of a whole. It is expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 3/4, the denominator (4) signifies that the whole is divided into four equal parts, and the numerator (3) indicates that we are considering three of those parts.
Fractions can be:
- Proper fractions: where the numerator is less than the denominator (e.g., 1/2, 3/4). These fractions represent a value less than 1.
- Improper fractions: where the numerator is greater than or equal to the denominator (e.g., 5/4, 7/7). These fractions represent a value greater than or equal to 1.
- Mixed numbers: a combination of a whole number and a proper fraction (e.g., 1 1/2). This represents a value greater than 1.
Understanding Decimals
A decimal is another way to represent a part of a whole. It uses a base-ten system, where each place value to the right of the decimal point represents a power of ten (tenths, hundredths, thousandths, and so on). For example, 0.75 represents 7 tenths and 5 hundredths, or 75/100.
Decimals can be easily converted to fractions and vice-versa. For instance, 0.75 is equivalent to 75/100, which can be simplified to 3/4 by dividing both the numerator and denominator by their greatest common divisor (25).
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of 100." Therefore, 75% means 75 out of 100, which can be written as the fraction 75/100 or the decimal 0.75.
Percentages are frequently used to represent proportions, rates, and changes. They provide a convenient way to compare different quantities expressed as parts of a whole.
The Relationship Between 75, 3/4, and 0.75
Now, let's address the central question: Is 75 the same as 3/4? The answer is: not directly, but they represent the same proportion or value. The number 75, in this context, implicitly represents 75%, which is equivalent to the fraction 75/100 and the decimal 0.75.
To demonstrate their equivalence:
- 75% as a fraction: 75% = 75/100
- Simplifying the fraction: 75/100 can be simplified by dividing both the numerator and denominator by their greatest common divisor (25): 75/100 = (75 ÷ 25) / (100 ÷ 25) = 3/4
- Fraction to decimal: 3/4 can be converted to a decimal by dividing the numerator (3) by the denominator (4): 3 ÷ 4 = 0.75
- Decimal to percentage: 0.75 can be converted to a percentage by multiplying by 100: 0.75 × 100 = 75%
Therefore, we have established the equivalence: 75% = 75/100 = 3/4 = 0.75
Practical Applications
Understanding the interchangeability of fractions, decimals, and percentages is crucial in various real-world scenarios, including:
- Calculating discounts: A 75% discount is the same as a 3/4 reduction.
- Determining proportions: If 3 out of 4 people prefer a certain product (3/4), this represents 75% preference.
- Measuring quantities: Three-quarters of a cup (3/4 cup) is equal to 0.75 cups.
- Financial calculations: Interest rates, tax calculations, and investment returns often involve the use of percentages, fractions, and decimals.
- Data analysis: Understanding these representations is essential for interpreting and presenting data effectively.
Common Mistakes and How to Avoid Them
A common mistake is confusing the whole number 75 with the fraction 3/4 or the percentage 75%. It's essential to remember that 75 represents a whole quantity, whereas 3/4 and 75% represent parts of a whole. Always pay attention to the context and the units involved.
Another common mistake is incorrectly simplifying fractions. Always divide both the numerator and the denominator by their greatest common divisor to obtain the simplest form of the fraction.
Finally, ensure accurate conversion between fractions, decimals, and percentages by following the steps outlined above. Double-checking your calculations helps minimize errors.
Advanced Concepts and Further Exploration
This foundational understanding can be built upon to explore more advanced concepts:
- Ratio and Proportion: Fractions are directly related to ratios and proportions, providing a powerful tool for solving problems involving comparative quantities.
- Algebraic Expressions: Fractions and decimals frequently appear in algebraic equations and expressions, requiring proficiency in manipulating them.
- Calculus: Understanding fractions and decimals is essential for working with derivatives and integrals in calculus.
Conclusion
While 75 and 3/4 are not directly identical, they represent the same value when 75 is understood as 75%. The ability to convert freely between fractions, decimals, and percentages is a fundamental skill in mathematics. Mastering these conversions empowers you to tackle a wide range of mathematical problems and confidently apply these concepts in real-world situations. By understanding their interconnectedness and employing careful calculation techniques, you can avoid common errors and ensure accurate results in any mathematical endeavor. The seemingly simple question of whether 75 is the same as 3/4 opens a door to a much broader understanding of numerical representation and mathematical manipulation.
Latest Posts
Latest Posts
-
How Many Mini Marshmallows Are In A Bag
Jul 16, 2025
-
How Many Times Has Thanksgiving Been On November 28
Jul 16, 2025
-
How Many Laps Around A Gym Is A Mile
Jul 16, 2025
-
How Far From Tampa To Cape Coral
Jul 16, 2025
-
1 Megawatt Can Power How Many Homes
Jul 16, 2025
Related Post
Thank you for visiting our website which covers about Is 75 The Same As 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.