Is -9 A Rational Number Or Irrational
Kalali
Mar 31, 2025 · 5 min read
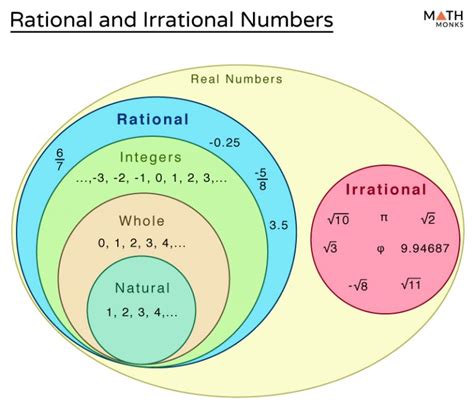
Table of Contents
Is -9 a Rational Number or Irrational? A Deep Dive into Number Classification
The question of whether -9 is a rational or irrational number might seem trivial at first glance. However, understanding the fundamental differences between these number types is crucial for grasping more advanced mathematical concepts. This article delves into the definition of rational and irrational numbers, provides a definitive answer regarding -9, and explores related concepts with practical examples.
Understanding Rational Numbers
A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where p is the numerator and q is the non-zero denominator. In simpler terms, it's a number that can be written as a fraction where both the top and bottom numbers are whole numbers (and the bottom number isn't zero).
Key characteristics of rational numbers:
- Expressible as a fraction: This is the defining characteristic. Examples include 1/2, 3/4, -5/7, and even whole numbers like 4 (which can be expressed as 4/1).
- Terminating or repeating decimals: When expressed as a decimal, rational numbers either terminate (end) or have a repeating pattern of digits. For example, 1/2 = 0.5 (terminating), and 1/3 = 0.333... (repeating).
- Inclusiveness: Rational numbers encompass integers, whole numbers, and natural numbers.
Examples of Rational Numbers
Let's illustrate with some examples:
- 1/2: This is a classic example. It's a fraction of two integers.
- -3: This can be written as -3/1, satisfying the definition.
- 0.75: This can be written as 3/4.
- 0.333...: This repeating decimal represents 1/3.
- 2.5: This can be written as 5/2.
Understanding Irrational Numbers
Irrational numbers are numbers that cannot be expressed as a fraction of two integers. Their decimal representations are non-terminating and non-repeating – they go on forever without any discernible pattern.
Key characteristics of irrational numbers:
- Non-fractional representation: This is the defining feature. They cannot be expressed as a simple fraction of two integers.
- Non-terminating, non-repeating decimals: Their decimal expansions continue infinitely without repeating sequences.
- Famous examples: The most well-known examples are π (pi) and √2 (the square root of 2).
Examples of Irrational Numbers
Here are some prominent examples:
- π (pi): Approximately 3.14159..., it's the ratio of a circle's circumference to its diameter. Its decimal expansion continues infinitely without repeating.
- √2 (square root of 2): Approximately 1.414..., it's the number which, when multiplied by itself, equals 2. Its decimal representation is non-terminating and non-repeating.
- e (Euler's number): Approximately 2.718..., it's a fundamental constant in calculus and other areas of mathematics. It's also irrational.
- The golden ratio (φ): Approximately 1.618..., It appears in various aspects of nature and art.
Is -9 a Rational Number or Irrational?
Now, let's address the central question: Is -9 a rational number or irrational?
The answer is unequivocally: -9 is a rational number.
Here's why:
-9 can be expressed as the fraction -9/1. This satisfies the definition of a rational number: it's the quotient of two integers (-9 and 1). The denominator is not zero.
Therefore, -9 fits perfectly within the category of rational numbers. It is an integer, and all integers are considered rational numbers.
Expanding on Number Sets and Their Relationships
To fully understand the classification of -9, let's examine the hierarchy of number sets:
- Natural Numbers (N): These are the counting numbers: 1, 2, 3, 4...
- Whole Numbers (W): These include natural numbers and zero: 0, 1, 2, 3...
- Integers (Z): These include whole numbers and their negative counterparts: ..., -3, -2, -1, 0, 1, 2, 3...
- Rational Numbers (Q): These encompass all numbers that can be expressed as a fraction of two integers. This includes integers, as we've seen.
- Irrational Numbers (I): These are numbers that cannot be expressed as a fraction of two integers.
- Real Numbers (R): This is the union of rational and irrational numbers. It encompasses all numbers that can be plotted on a number line.
The relationships between these sets can be visualized as nested sets, where each set contains the previous ones: N ⊂ W ⊂ Z ⊂ Q ⊂ R. Irrational numbers (I) are also a subset of real numbers (R), but they are disjoint from rational numbers (Q).
Practical Applications and Importance of Number Classification
Understanding the distinction between rational and irrational numbers is not merely an academic exercise. It has significant practical applications across various fields:
- Computer Science: Representing rational numbers in computers is generally straightforward, as they can be stored as fractions. Irrational numbers, however, require approximations, which can lead to rounding errors and inaccuracies in computations.
- Engineering: Precise calculations in engineering often involve rational numbers. However, understanding the limitations of representing irrational numbers in calculations is crucial for ensuring accuracy and safety in design and construction.
- Physics: Many physical constants, like the speed of light or gravitational constant, are often approximated using rational numbers for practical calculations.
- Finance: While financial calculations primarily use rational numbers, understanding the limitations of decimal representation can be crucial in avoiding rounding errors in large-scale financial transactions.
Conclusion: The Rationality of -9
In conclusion, -9 is definitively a rational number. Its expressibility as a fraction (-9/1) directly satisfies the definition of a rational number. This understanding reinforces a foundational concept in mathematics and highlights the importance of correctly classifying numbers to ensure accuracy and efficiency in various applications. The broader context of number sets and their relationships further enriches this understanding and underscores the interconnectedness of mathematical concepts. The ability to confidently differentiate between rational and irrational numbers is a vital skill for anyone pursuing further studies or practical applications in mathematics and related fields. Remembering the key characteristics—fractional representation for rational numbers and non-terminating, non-repeating decimals for irrational numbers—will solidify this crucial mathematical foundation.
Latest Posts
Latest Posts
-
37 Degrees Fahrenheit Is What In Celsius
Apr 02, 2025
-
Cuanto Es 80 Pulgadas En Pies
Apr 02, 2025
-
1 7 Meters Is How Many Feet
Apr 02, 2025
-
How Long Can Cats Hold Their Breath Underwater
Apr 02, 2025
-
28 Out Of 50 As A Percentage
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Is -9 A Rational Number Or Irrational . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
