Is Ax_1 Bx_2 Cx_3 Dx_4 A Line
Kalali
May 24, 2025 · 3 min read
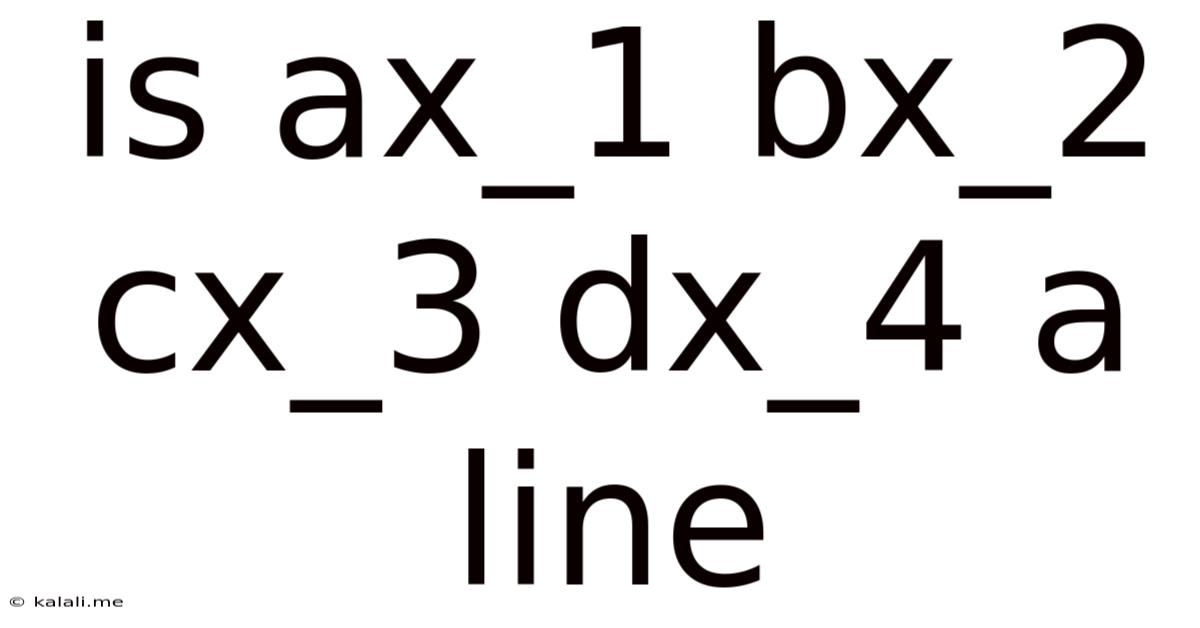
Table of Contents
Is ax₁ + bx₂ + cx₃ + dx₄ = 0 a Line? A Deep Dive into Hyperplanes and Linear Algebra
This article explores the geometric interpretation of the equation ax₁ + bx₂ + cx₃ + dx₄ = 0, specifically addressing whether it represents a line. The short answer is: no, not in the typical sense of a line in 2D or 3D space. However, it represents a fundamental geometric object in higher dimensions. This equation describes a hyperplane in four-dimensional space.
This equation involves four variables (x₁, x₂, x₃, x₄), implying a four-dimensional space (ℝ⁴). A line, as we typically visualize it, exists in two or three dimensions. To understand this better, let's break down the concept of dimensionality and hyperplanes.
Understanding Dimensionality and Geometric Objects
- 2D (Two-dimensional space): A line is defined by a single equation of the form
ax + by + c = 0. It divides the plane into two half-planes. - 3D (Three-dimensional space): A plane is defined by a single equation of the form
ax + by + cz + d = 0. It divides the 3D space into two half-spaces. A line in 3D is defined by the intersection of two planes (requiring two equations). - 4D (Four-dimensional space): The equation
ax₁ + bx₂ + cx₃ + dx₄ = 0defines a hyperplane. This is a three-dimensional subspace within the four-dimensional space. Think of it as the 3D equivalent of a plane in 3D space, but existing in a higher dimension. It divides the 4D space into two regions.
Hyperplanes: The Generalization to Higher Dimensions
A hyperplane is a generalization of lines and planes to higher dimensions. In n-dimensional space, a hyperplane is defined by a single linear equation of the form:
a₁x₁ + a₂x₂ + ... + aₙxₙ + b = 0
Where:
a₁, a₂, ..., aₙare constants (coefficients).x₁, x₂, ..., xₙare variables representing the coordinates inn-dimensional space.bis a constant.
Visualizing a Hyperplane (Challenging, but Possible)
Visualizing a hyperplane directly is difficult, as we are limited to three spatial dimensions. However, we can understand its properties through analogy and mathematical reasoning. It's a flat, three-dimensional object within four-dimensional space, dividing that space into two regions.
Finding Points on the Hyperplane
To find points that lie on the hyperplane defined by ax₁ + bx₂ + cx₃ + dx₄ = 0, we need to find sets of values for x₁, x₂, x₃, and x₄ that satisfy the equation. There are infinitely many such sets, just as there are infinitely many points on a line or plane.
For example, if a=1, b=2, c=3, d=-4, then the point (1, 1, 1, 1) would not lie on the hyperplane since 1 + 2(1) + 3(1) - 4(1) = 2 ≠ 0. However, the point (0, 0, 0, 0) satisfies the equation, indicating it resides on the hyperplane.
Conclusion
In summary, ax₁ + bx₂ + cx₃ + dx₄ = 0 does not represent a line in the conventional sense. Instead, it describes a hyperplane, a three-dimensional subspace within a four-dimensional space. Understanding hyperplanes requires extending our geometric intuition beyond three dimensions, embracing the concepts of linear algebra and higher-dimensional geometry. The equation represents a fundamental structure in linear algebra and has significant applications in various fields, including machine learning and data analysis.
Latest Posts
Latest Posts
-
Can You Bring Electric Shaver On Plane
May 24, 2025
-
Why Does My Toilet Keep Clogging
May 24, 2025
-
Do With That What You Will
May 24, 2025
-
How To Get Squirrels Out Of Attic
May 24, 2025
-
How Many Ounces Is A Cup Of Cheese
May 24, 2025
Related Post
Thank you for visiting our website which covers about Is Ax_1 Bx_2 Cx_3 Dx_4 A Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.