Lcm Of 12 15 And 10
Kalali
Jun 11, 2025 · 3 min read
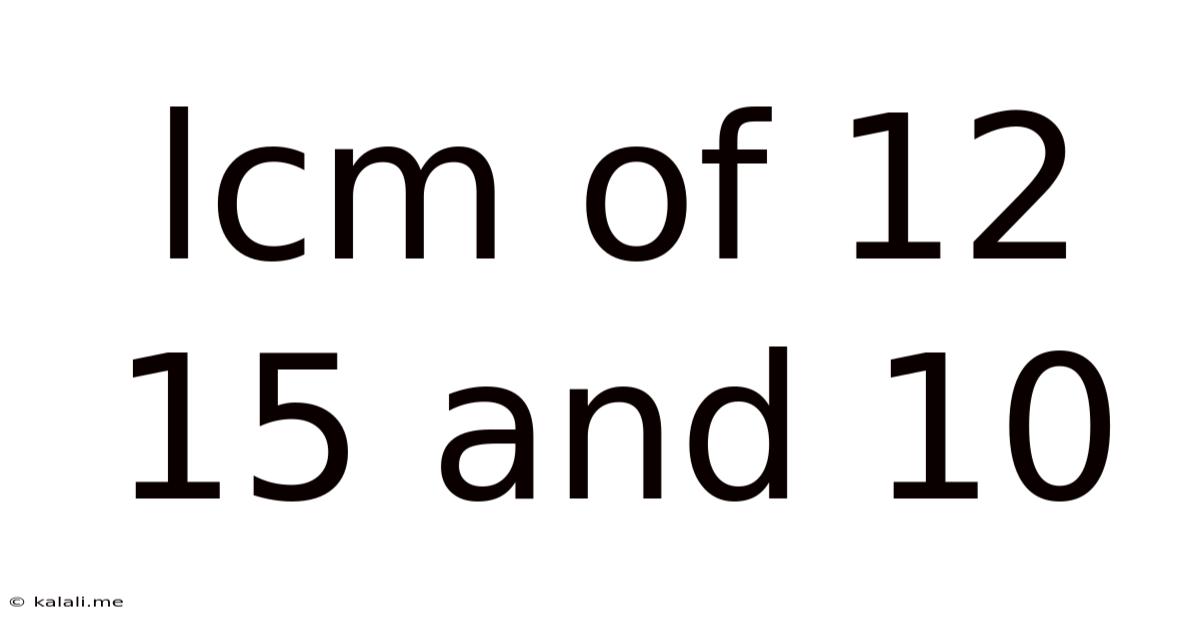
Table of Contents
Finding the Least Common Multiple (LCM) of 12, 15, and 10
Finding the least common multiple (LCM) is a fundamental concept in mathematics, frequently used in various applications from scheduling to simplifying fractions. This article will guide you through the process of calculating the LCM of 12, 15, and 10, explaining the different methods and highlighting their advantages. Understanding LCM is crucial for anyone working with fractions, ratios, or problems involving cyclical events.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. This concept is particularly helpful when working with fractions, allowing you to find a common denominator for addition and subtraction.
Methods for Calculating LCM of 12, 15, and 10
There are several ways to determine the LCM. Let's explore two common methods:
1. Prime Factorization Method
This method involves breaking down each number into its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, etc.).
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
- Prime factorization of 15: 3 x 5
- Prime factorization of 10: 2 x 5
Next, identify the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Finally, multiply these highest powers together: 4 x 3 x 5 = 60
Therefore, the LCM of 12, 15, and 10 is 60.
2. Listing Multiples Method
This method is simpler for smaller numbers but can become less efficient with larger numbers. It involves listing the multiples of each number until you find the smallest common multiple.
- Multiples of 12: 12, 24, 36, 48, 60, 72...
- Multiples of 15: 15, 30, 45, 60, 75...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70...
The smallest number that appears in all three lists is 60. Therefore, the LCM of 12, 15, and 10 is 60.
Which Method is Best?
The prime factorization method is generally more efficient, especially when dealing with larger numbers or a greater number of integers. The listing multiples method is easier to grasp initially but can become tedious and impractical for larger numbers.
Applications of LCM
Understanding LCM has practical applications in various areas, including:
- Fraction addition and subtraction: Finding a common denominator.
- Scheduling: Determining when events will coincide (e.g., buses arriving at a stop).
- Measurement conversions: Simplifying units of measurement.
- Pattern recognition: Identifying repeating cycles.
By mastering the calculation of the least common multiple, you equip yourself with a valuable tool for solving mathematical problems across numerous disciplines. The LCM of 12, 15, and 10, as demonstrated, is a straightforward yet illustrative example of this important concept.
Latest Posts
Latest Posts
-
How Many Ounces In A Pint Of Blueberries
Jul 01, 2025
-
When Derivatively Classifying Information Where Can You Find A Listing
Jul 01, 2025
-
How Many Hours Is 9am To 1pm
Jul 01, 2025
-
How Fast Is 200 Km Per Hour
Jul 01, 2025
-
How Many Babies Were Conceived At Woodstock 1969
Jul 01, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 12 15 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.