Lcm Of 2 5 And 6
Kalali
Jun 15, 2025 · 3 min read
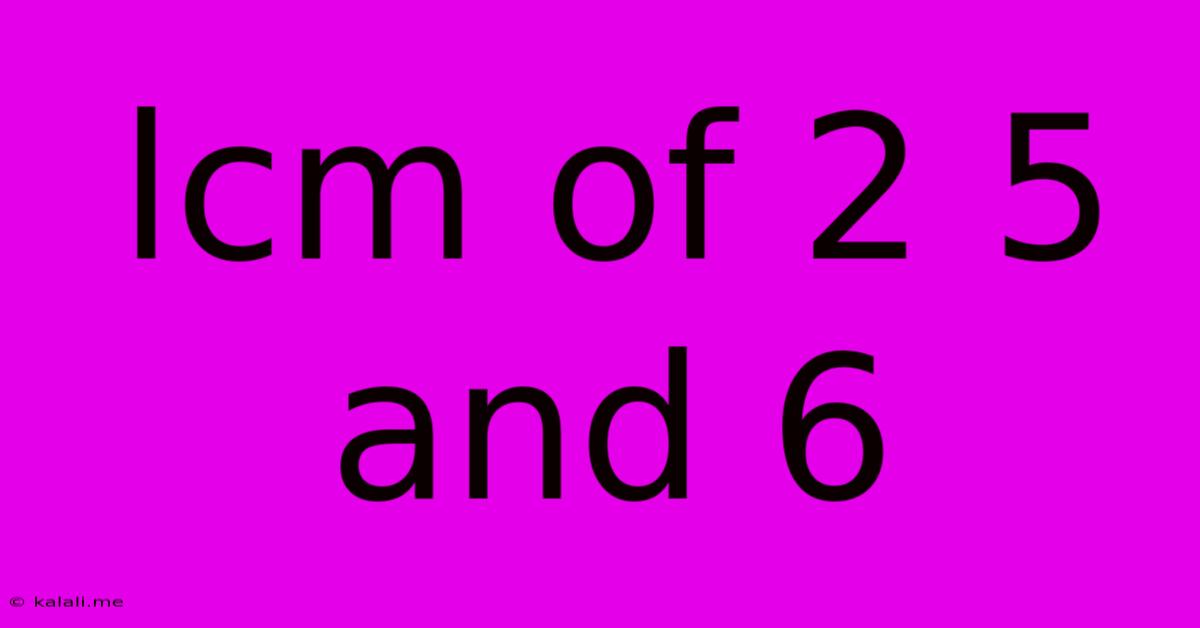
Table of Contents
Finding the Least Common Multiple (LCM) of 2, 5, and 6
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly useful in simplifying fractions and solving problems involving cycles or repeating events. This article will guide you through calculating the LCM of 2, 5, and 6 using different methods, explaining the process clearly and concisely. Understanding how to find the LCM is crucial for various mathematical applications, from basic arithmetic to advanced algebra. This guide will demystify the process and equip you with the knowledge to tackle similar problems with confidence.
Understanding Least Common Multiple
The least common multiple (LCM) is the smallest positive integer that is divisible by all the numbers in a given set. In simpler terms, it's the smallest number that all the numbers in the set can divide into evenly. This differs from the greatest common divisor (GCD), which is the largest number that divides all numbers in the set without leaving a remainder.
Method 1: Listing Multiples
One way to find the LCM of 2, 5, and 6 is by listing the multiples of each number until you find the smallest common multiple.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35...
- Multiples of 6: 6, 12, 18, 24, 30, 36...
By comparing the lists, we can see that the smallest number appearing in all three lists is 30. Therefore, the LCM of 2, 5, and 6 is 30. This method is straightforward for smaller numbers but can become cumbersome for larger numbers.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, is to use prime factorization. This involves breaking down each number into its prime factors.
- Prime factorization of 2: 2
- Prime factorization of 5: 5
- Prime factorization of 6: 2 x 3
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Now, multiply these highest powers together: 2 x 3 x 5 = 30. This confirms that the LCM of 2, 5, and 6 is indeed 30. This method is generally faster and more efficient than listing multiples, especially when dealing with larger numbers or a greater number of integers.
Method 3: Using the Formula (for two numbers)
While not directly applicable to three numbers without modification, understanding the formula for two numbers is beneficial. The formula states: LCM(a, b) = (|a * b|) / GCD(a, b), where GCD is the greatest common divisor. To use this for three or more numbers, you'd need to find the LCM of two numbers first, then find the LCM of the result and the third number, and so on.
Conclusion
This article has demonstrated three methods for finding the least common multiple of 2, 5, and 6. The prime factorization method is generally the most efficient, particularly when dealing with larger numbers. Understanding these methods provides a strong foundation for tackling more complex problems involving LCM and GCD in various mathematical contexts. Remember to choose the method that best suits the numbers you're working with for optimal efficiency.
Latest Posts
Latest Posts
-
Select All Of The Following That Are True About Marsupials
Jun 16, 2025
-
What Is Conjugate Base Of H2po4
Jun 16, 2025
-
Johnson And Wales University Gpa Requirements
Jun 16, 2025
-
National Film Award For Best Music Direction
Jun 16, 2025
-
How Many Bytes Is 1 Tb
Jun 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 5 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.