Lcm Of 3 4 And 8
Kalali
Jun 15, 2025 · 2 min read
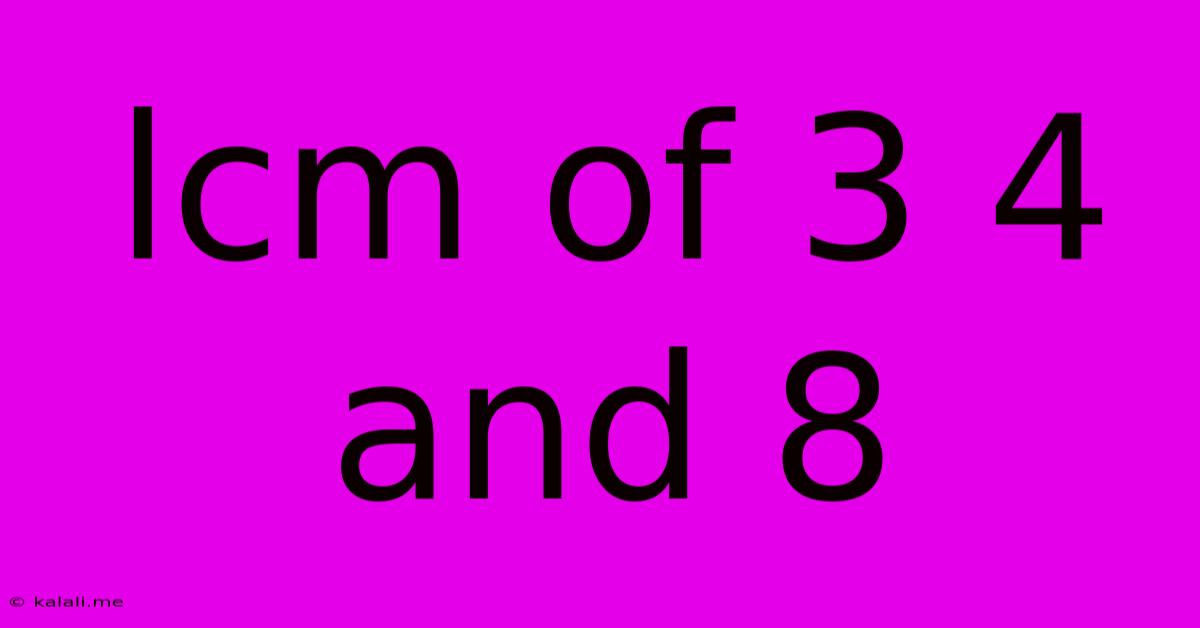
Table of Contents
Finding the LCM of 3, 4, and 8: A Step-by-Step Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, particularly useful in algebra and number theory. This guide will walk you through calculating the LCM of 3, 4, and 8, explaining the methods and underlying principles. Understanding LCM is crucial for simplifying fractions, solving problems involving ratios and proportions, and even in more advanced mathematical concepts.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) is the smallest positive integer that is divisible by all the numbers in a given set. In simpler terms, it's the smallest number that all the numbers in the set can divide into evenly. This contrasts with the greatest common divisor (GCD), which is the largest number that divides all the numbers in a set without leaving a remainder.
Methods for Finding the LCM of 3, 4, and 8
There are several ways to calculate the LCM. Let's explore two common methods:
Method 1: Listing Multiples
This method is straightforward, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32...
- Multiples of 8: 8, 16, 24, 32, 40...
By comparing the lists, we see that the smallest multiple common to all three numbers is 24. Therefore, the LCM of 3, 4, and 8 is 24.
Method 2: Prime Factorization
This method is more efficient for larger numbers or when dealing with more numbers in the set. It involves breaking down each number into its prime factors:
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 8: 2 x 2 x 2 = 2³
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
Now, we multiply these highest powers together: 8 x 3 = 24. This confirms that the LCM of 3, 4, and 8 is indeed 24.
Understanding the Result
The LCM of 3, 4, and 8 being 24 means that 24 is the smallest number that is divisible by 3, 4, and 8 without leaving a remainder. This fact is useful in various applications, such as finding a common denominator when adding or subtracting fractions with denominators 3, 4, and 8.
Conclusion:
Calculating the LCM is a valuable skill in mathematics. Whether you use the method of listing multiples or prime factorization, understanding the concept and applying the correct method will help you solve problems involving least common multiples efficiently. Remember that the prime factorization method becomes increasingly advantageous when dealing with larger numbers or a greater number of integers.
Latest Posts
Latest Posts
-
Freezing Point Of Water In Celsius And Fahrenheit
Jun 15, 2025
-
What Cell Organelle Carries Out Cellular Respiration
Jun 15, 2025
-
Which Game Was Invented In India
Jun 15, 2025
-
Which Of The Following Is A First Class Lever
Jun 15, 2025
-
The Atomic Mass Number Is Equal To
Jun 15, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 4 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.