Lcm Of 3 5 And 10
Kalali
Jun 11, 2025 · 3 min read
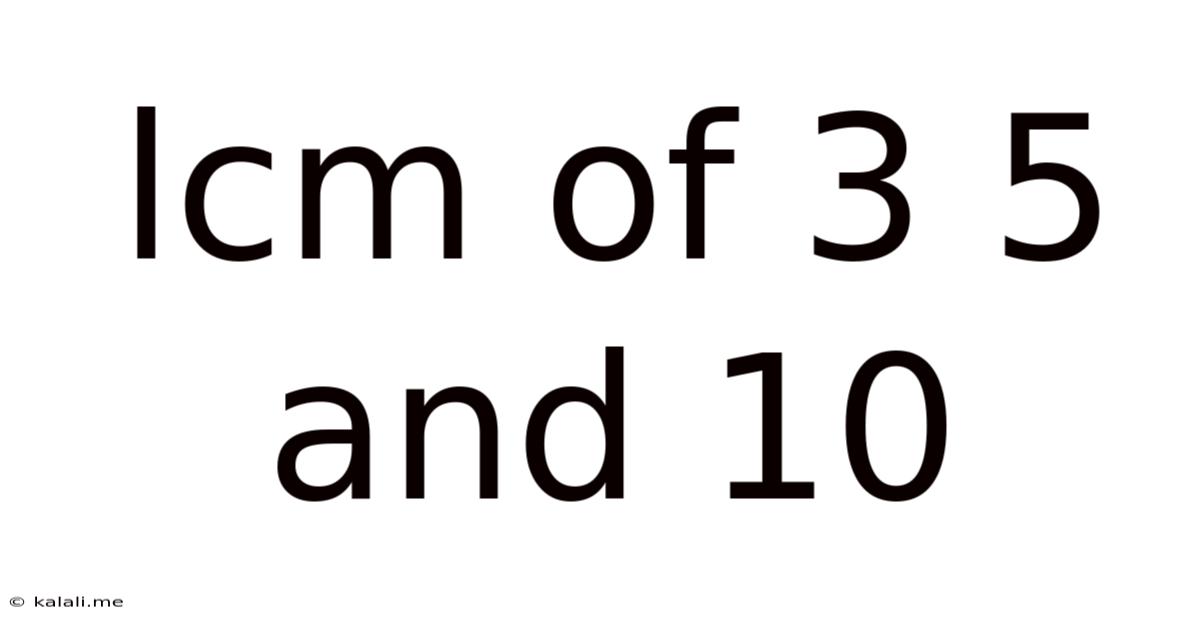
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 5, and 10
This article will guide you through the process of calculating the Least Common Multiple (LCM) of 3, 5, and 10. Understanding LCM is crucial in various mathematical applications, from simplifying fractions to solving problems involving cycles and patterns. We'll explore different methods to find the LCM, making it easy to understand regardless of your mathematical background.
What is the Least Common Multiple (LCM)?
The Least Common Multiple (LCM) is the smallest positive integer that is a multiple of all the integers in a given set. In simpler terms, it's the smallest number that can be divided evenly by all the numbers in the set without leaving a remainder. For example, the LCM of 2 and 3 is 6, because 6 is the smallest number divisible by both 2 and 3.
Method 1: Listing Multiples
One straightforward approach is to list the multiples of each number until you find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 5: 5, 10, 15, 20, 25, 30...
- Multiples of 10: 10, 20, 30...
By comparing the lists, we see that the smallest number present in all three lists is 30. Therefore, the LCM of 3, 5, and 10 is 30. This method works well for smaller numbers, but can become cumbersome with larger numbers.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, involves prime factorization. This method breaks down each number into its prime factors.
-
Prime Factorization:
- 3 = 3
- 5 = 5
- 10 = 2 x 5
-
Identify the highest power of each prime factor: We have the prime factors 2, 3, and 5. The highest power of 2 is 2¹ (from 10), the highest power of 3 is 3¹ (from 3), and the highest power of 5 is 5¹ (from 5 and 10).
-
Multiply the highest powers together: 2¹ x 3¹ x 5¹ = 30
Therefore, using prime factorization, we again find that the LCM of 3, 5, and 10 is 30. This method is generally more efficient and less prone to errors than listing multiples, especially when dealing with larger numbers or a greater number of integers.
Applications of LCM
The concept of LCM has broad applications across various fields:
- Fractions: Finding the LCM of denominators is essential when adding or subtracting fractions.
- Scheduling: Determining when events with different periodicities will coincide (e.g., when two machines will need maintenance at the same time).
- Modular Arithmetic: Used in cryptography and other areas of mathematics.
- Music Theory: Understanding rhythms and musical intervals.
Conclusion
Finding the LCM of 3, 5, and 10 demonstrates the application of fundamental mathematical concepts. Whether you use the method of listing multiples or prime factorization, the result remains consistent: the LCM of 3, 5, and 10 is 30. Understanding these methods provides a solid foundation for tackling more complex LCM problems and related mathematical challenges. Remember that choosing the most efficient method depends on the context and the size of the numbers involved.
Latest Posts
Latest Posts
-
How Old Are You If Your Born In 1988
Jul 01, 2025
-
How Many Quarts Are In 18 Gallons
Jul 01, 2025
-
How Old Are You If You Were Born In 2002
Jul 01, 2025
-
How Many Sides Does A Star Have
Jul 01, 2025
-
How Many Ears Of Corn In A Can
Jul 01, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 5 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.