Lcm Of 3 8 And 12
Kalali
Jun 11, 2025 · 3 min read
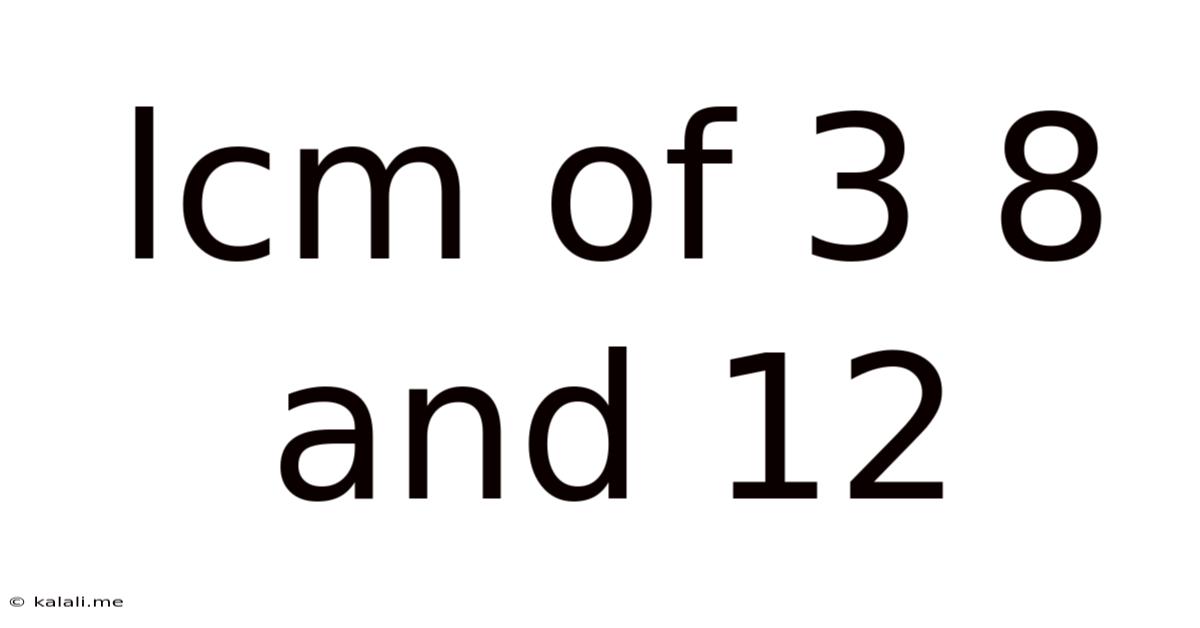
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 8, and 12
This article will guide you through calculating the least common multiple (LCM) of 3, 8, and 12. Understanding LCM is crucial in various mathematical applications, from simplifying fractions to solving problems involving cyclical events. We'll explore different methods to find the LCM, ensuring you understand the process completely. This will also cover related concepts like prime factorization and greatest common divisor (GCD).
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of a set of numbers is the smallest positive integer that is a multiple of all the numbers in the set. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, the LCM of 2 and 3 is 6, because 6 is the smallest number divisible by both 2 and 3.
Method 1: Listing Multiples
This method is straightforward for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 8: 8, 16, 24, 32, 40...
- Multiples of 12: 12, 24, 36, 48...
Notice that 24 appears in all three lists. Therefore, the LCM of 3, 8, and 12 is 24.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a more structured approach. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
-
Find the prime factorization of each number:
- 3 = 3
- 8 = 2³
- 12 = 2² x 3
-
Identify the highest power of each prime factor:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
-
Multiply the highest powers together: 8 x 3 = 24
Therefore, the LCM of 3, 8, and 12 is 24.
Method 3: Using the GCD (Greatest Common Divisor)
The LCM and GCD are related. You can find the LCM using the GCD with the following formula:
LCM(a, b, c) = (a x b x c) / GCD(a, b, c)
However, this formula is most easily applied to two numbers. To find the LCM of three or more numbers, you would need to find the LCM of two, then the LCM of that result and the third number, and so on. For this example, it’s less efficient than the previous methods.
Applications of LCM
The LCM has various real-world applications:
- Scheduling: Determining when events will occur simultaneously. For example, if three events occur every 3, 8, and 12 days respectively, they will all occur together again in 24 days.
- Fractions: Finding the least common denominator when adding or subtracting fractions.
- Measurement: Converting units of measurement.
Conclusion
We've explored three different methods to find the LCM of 3, 8, and 12. The prime factorization method is generally the most efficient for larger numbers, offering a systematic approach. Remember to choose the method that best suits the numbers involved and your comfort level. Understanding LCM is a fundamental skill with broad applications across mathematics and beyond.
Latest Posts
Latest Posts
-
Which One Of The Gatlin Brothers Passed Away
Jul 01, 2025
-
Do Naked And Afraid Contestants Get Paid
Jul 01, 2025
-
How Many Bottles Of Water Is 64 Oz
Jul 01, 2025
-
Was Brigham Young Stabbed By One Of His Sons
Jul 01, 2025
-
How Much Does 2 Liters Of Water Weigh
Jul 01, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 8 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.