Lcm Of 6 8 And 9
Kalali
Jun 15, 2025 · 3 min read
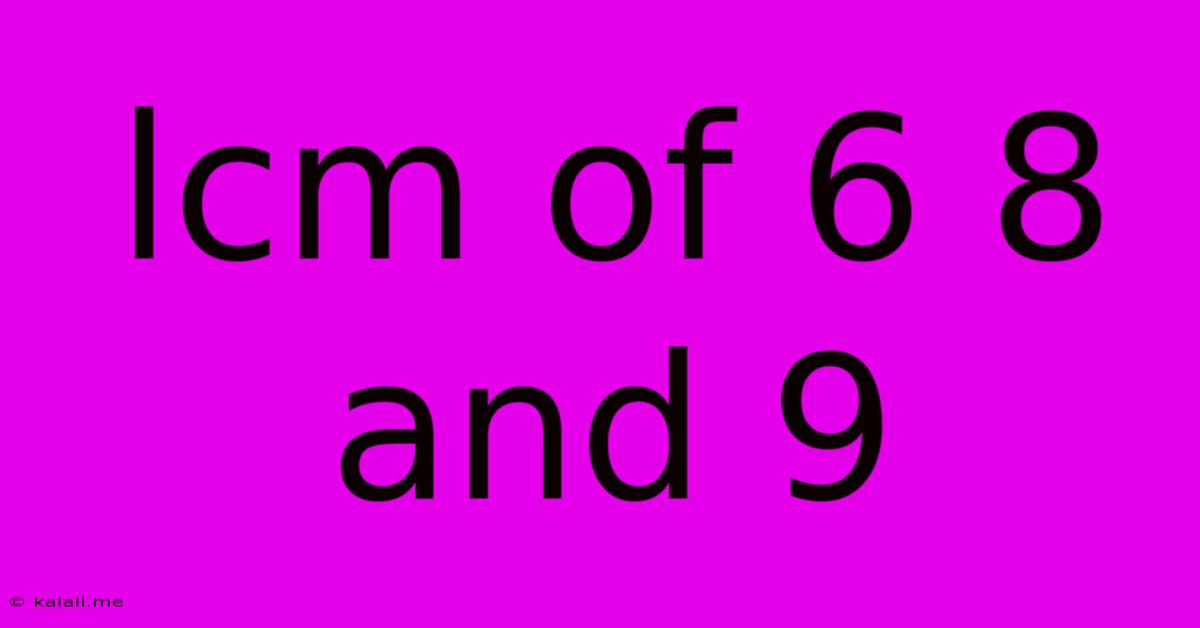
Table of Contents
Finding the Least Common Multiple (LCM) of 6, 8, and 9
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, particularly useful in areas like fractions, scheduling, and various other applications. This article will guide you through the process of calculating the LCM of 6, 8, and 9, using several methods. Understanding these methods will empower you to find the LCM of any set of numbers efficiently. This will also cover related concepts such as prime factorization and greatest common divisor (GCD).
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, the LCM of 2 and 3 is 6, because 6 is the smallest number divisible by both 2 and 3.
Methods for Finding the LCM of 6, 8, and 9
We'll explore two primary methods to determine the LCM of 6, 8, and 9:
1. Prime Factorization Method
This method involves breaking down each number into its prime factors. Prime factors are numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, etc.).
- Prime factorization of 6: 2 x 3
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 9: 3 x 3 = 3²
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3² = 9
Now, multiply these highest powers together: 8 x 9 = 72
Therefore, the LCM of 6, 8, and 9 is 72.
2. Listing Multiples Method
This method involves listing the multiples of each number until you find the smallest common multiple. While effective for smaller numbers, it becomes less efficient with larger numbers.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, ...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, ...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, ...
By comparing the lists, we can see that the smallest common multiple is 72.
Relationship between LCM and GCD
The greatest common divisor (GCD) is the largest number that divides all the given numbers without leaving a remainder. There's a useful relationship between the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
This formula works for two numbers. For more than two numbers, the calculation becomes slightly more complex but the concept remains relevant.
Conclusion
Finding the LCM is a valuable skill with various applications. The prime factorization method is generally more efficient, especially when dealing with larger numbers. Understanding both methods provides flexibility and a deeper understanding of the concept of least common multiples. Remember that the LCM of 6, 8, and 9 is definitively 72.
Latest Posts
Latest Posts
-
Square Root Of 208 In Radical Form
Jun 16, 2025
-
Lithium Ion Battery Advantages And Disadvantages
Jun 16, 2025
-
Semiconductors Have How Many Electrons In Their Valence Rings
Jun 16, 2025
-
Moment Of Inertia Of A Disk With A Hole
Jun 16, 2025
-
What Medium Does Light Travel Fastest Through
Jun 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 6 8 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.