Least Common Factor Of 8 And 9
Kalali
Apr 03, 2025 · 5 min read
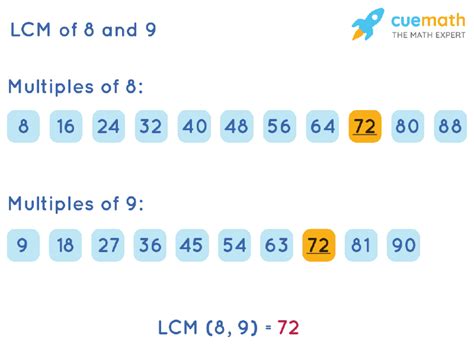
Table of Contents
- Least Common Factor Of 8 And 9
- Table of Contents
- Unveiling the Least Common Multiple (LCM) of 8 and 9: A Deep Dive into Number Theory
- Understanding the Concept of Least Common Multiple (LCM)
- Method 1: Listing Multiples
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81...
- Method 2: Prime Factorization
- Prime Factorization of 8:
- Prime Factorization of 9:
- Method 3: Using the Greatest Common Divisor (GCD)
- Applications of LCM in Real-World Scenarios
- Expanding the Concept: LCM of More Than Two Numbers
- Conclusion: The Significance of LCM in Mathematics and Beyond
- Latest Posts
- Related Post
Unveiling the Least Common Multiple (LCM) of 8 and 9: A Deep Dive into Number Theory
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a deeper appreciation for number theory and its applications. This comprehensive guide will delve into the process of calculating the LCM of 8 and 9, exploring different methods and illuminating the theoretical foundations that govern this fundamental concept. We'll move beyond the simple calculation to explore the broader implications of LCM in various mathematical fields.
Understanding the Concept of Least Common Multiple (LCM)
Before diving into the specifics of finding the LCM of 8 and 9, let's establish a solid understanding of what LCM actually represents. The least common multiple of two or more integers is the smallest positive integer that is a multiple of each of the integers. In simpler terms, it's the smallest number that both (or all) of the given numbers can divide into evenly. This concept is crucial in various areas, from simplifying fractions to solving problems involving rhythmic cycles or scheduling events.
Method 1: Listing Multiples
One of the most straightforward methods for finding the LCM of relatively small numbers like 8 and 9 is by listing their multiples until a common multiple is found.
Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80...
Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81...
By inspecting the lists, we observe that the smallest number appearing in both lists is 72. Therefore, the LCM of 8 and 9 is 72. This method works well for small numbers, but it becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
A more efficient and systematic approach to finding the LCM, particularly for larger numbers, involves prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
Prime Factorization of 8:
8 = 2 x 2 x 2 = 2³
Prime Factorization of 9:
9 = 3 x 3 = 3²
To find the LCM using prime factorization, we identify the highest power of each prime factor present in the factorizations of both numbers.
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3² = 9
We then multiply these highest powers together:
LCM(8, 9) = 2³ x 3² = 8 x 9 = 72
This method provides a more elegant and efficient solution, especially when dealing with larger numbers or multiple numbers simultaneously.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are intimately related. The GCD is the largest number that divides both numbers without leaving a remainder. There's a handy formula that connects the LCM and GCD:
LCM(a, b) = (|a x b|) / GCD(a, b)
where |a x b| represents the absolute value of the product of a and b.
Let's find the GCD of 8 and 9 using the Euclidean algorithm:
- Divide the larger number (9) by the smaller number (8): 9 ÷ 8 = 1 with a remainder of 1.
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (1).
- Repeat the division: 8 ÷ 1 = 8 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 1.
Now, we can use the formula:
LCM(8, 9) = (8 x 9) / GCD(8, 9) = 72 / 1 = 72
This method elegantly connects the concepts of LCM and GCD, providing another efficient way to calculate the LCM.
Applications of LCM in Real-World Scenarios
The concept of LCM extends far beyond the realm of abstract mathematics. Its applications are surprisingly diverse and relevant to many real-world problems:
-
Scheduling and Synchronization: Imagine two buses that depart from the same station at different intervals. The LCM of their departure intervals will determine when they both depart simultaneously again. This principle extends to scheduling meetings, coordinating shifts, or managing any cyclical process.
-
Fractions and Simplification: When adding or subtracting fractions, finding the LCM of the denominators is crucial for finding a common denominator, simplifying the calculation, and obtaining the most accurate result.
-
Rhythmic Patterns and Music: In music theory, the LCM helps determine when rhythmic patterns repeat simultaneously. Understanding the LCM of different rhythmic values allows composers and musicians to create complex and harmonious compositions.
-
Gear Ratios and Mechanical Systems: In engineering and mechanics, understanding the LCM helps in designing gear ratios for optimal performance and minimizing wear and tear.
-
Cyclic Processes in Nature: Many natural phenomena exhibit cyclical patterns, such as the phases of the moon, the orbits of planets, or biological rhythms. The LCM can help predict the simultaneous occurrence of these cycles.
Expanding the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. The prime factorization method remains particularly efficient. For example, to find the LCM of 8, 9, and 12:
-
Prime Factorization:
- 8 = 2³
- 9 = 3²
- 12 = 2² x 3
-
Identify Highest Powers:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3² = 9
-
Calculate LCM:
- LCM(8, 9, 12) = 2³ x 3² = 8 x 9 = 72
The LCM of 8, 9, and 12 is 72.
Conclusion: The Significance of LCM in Mathematics and Beyond
The seemingly simple task of finding the least common multiple of 8 and 9 opens a gateway to a fascinating world of number theory. Understanding the various methods for calculating the LCM, from listing multiples to employing prime factorization and utilizing the relationship with the GCD, equips us with valuable tools for tackling more complex mathematical problems. Moreover, the far-reaching applications of LCM demonstrate its practical significance in diverse fields, highlighting the interconnectedness of mathematical concepts and their relevance to the real world. This exploration underscores the beauty and power of mathematics in solving problems and understanding the world around us. By grasping the fundamental concept of LCM, we gain a deeper appreciation for the elegance and utility of number theory.
Latest Posts
Related Post
Thank you for visiting our website which covers about Least Common Factor Of 8 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.