Least Common Multiple 9 And 7
Kalali
Apr 06, 2025 · 5 min read
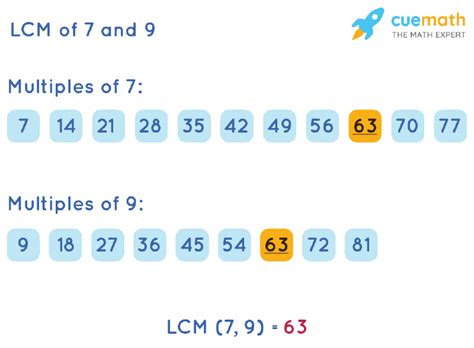
Table of Contents
Finding the Least Common Multiple (LCM) of 9 and 7: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications in various fields, from scheduling problems to music theory. This article delves into the intricacies of finding the LCM, focusing specifically on the LCM of 9 and 7. We will explore multiple methods, discuss their underlying principles, and highlight the importance of understanding LCM in different contexts.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 9 and 7, let's establish a solid understanding of the concept. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
It's crucial to differentiate the LCM from the greatest common divisor (GCD). While the LCM finds the smallest common multiple, the GCD identifies the largest common divisor. Both concepts are interconnected and often used together in various mathematical problems.
Methods for Calculating LCM
Several methods can be employed to calculate the LCM. We will explore three prominent approaches: the listing method, the prime factorization method, and the formula method.
1. The Listing Method
The listing method is a straightforward approach, particularly useful for smaller numbers. It involves listing the multiples of each number until a common multiple is found. The smallest common multiple is the LCM.
Let's apply this to 9 and 7:
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, ...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, ...
As you can see, the smallest common multiple of 9 and 7 is 63. Therefore, the LCM(9, 7) = 63. This method is effective for smaller numbers, but it becomes less efficient as the numbers grow larger.
2. The Prime Factorization Method
The prime factorization method provides a more systematic and efficient approach, especially when dealing with larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
- Prime factorization of 9: 3²
- Prime factorization of 7: 7
Since 9 and 7 have no common prime factors, the LCM is simply the product of their prime factorizations: 3² * 7 = 63. Therefore, LCM(9, 7) = 63. This method is more efficient than the listing method, especially when dealing with larger numbers with multiple prime factors.
3. The Formula Method
The formula method leverages the relationship between the LCM and the GCD (Greatest Common Divisor). The formula states:
LCM(a, b) * GCD(a, b) = a * b
Where 'a' and 'b' are the two integers.
To use this method, we first need to find the GCD of 9 and 7. Since 9 and 7 are coprime (they have no common factors other than 1), their GCD is 1.
Substituting into the formula:
LCM(9, 7) * GCD(9, 7) = 9 * 7 LCM(9, 7) * 1 = 63 LCM(9, 7) = 63
This method is efficient when the GCD is easily determined. For larger numbers, finding the GCD might require the Euclidean algorithm or other GCD-finding techniques.
Applications of LCM
The concept of LCM finds practical applications in diverse fields:
1. Scheduling Problems
Imagine two buses depart from a station at regular intervals. One bus departs every 9 minutes, and the other departs every 7 minutes. To find when both buses depart simultaneously, you need to find the LCM of 9 and 7. The LCM (63 minutes) represents the time when both buses will depart together again.
2. Fraction Operations
LCM is crucial when adding or subtracting fractions with different denominators. To find a common denominator, you need to find the LCM of the denominators.
For example, adding 1/9 and 1/7 requires finding the LCM of 9 and 7, which is 63. The fractions then become 7/63 and 9/63, easily added to get 16/63.
3. Music Theory
In music, LCM plays a role in determining the rhythmic patterns and harmonies. The LCM helps synchronize different musical phrases or rhythms with varying lengths.
4. Gear Ratios
In mechanical engineering, LCM is used in calculating gear ratios and other mechanical systems with different rotational speeds.
5. Cyclic Processes
LCM is relevant in any situation involving cyclic processes that repeat at different intervals. Finding the LCM helps determine when the cycles will align or coincide.
Advanced Concepts and Extensions
The concept of LCM extends beyond two numbers. You can find the LCM of multiple integers using similar methods, although the complexity increases with the number of integers. For instance, finding the LCM of 9, 7, and 5 would involve finding the prime factorization of each number and then multiplying the highest powers of each unique prime factor present.
The LCM also has connections to other mathematical concepts like modular arithmetic and abstract algebra.
Conclusion
Finding the least common multiple of 9 and 7, as demonstrated above, highlights the versatility and importance of LCM in various mathematical and real-world contexts. Understanding the different methods for calculating LCM – listing, prime factorization, and the formula method – equips you with the tools to tackle LCM problems effectively. Whether you're solving scheduling problems, simplifying fractions, or exploring more advanced mathematical concepts, a firm grasp of LCM is invaluable. Remember to choose the most efficient method based on the numbers involved to ensure accuracy and expediency. The ability to efficiently compute LCM is a fundamental skill for anyone working with numbers and mathematical applications.
Latest Posts
Latest Posts
-
What Is A 18 Out Of 30
Apr 07, 2025
-
What Is 30 Percent Of 15
Apr 07, 2025
-
How Many Inches Is 164 Cm
Apr 07, 2025
-
How Long Is 40 Inches In Cm
Apr 07, 2025
-
12 Cups Equals How Many Quarts
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple 9 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.