Least Common Multiple Of 12 And 6
Kalali
Apr 01, 2025 · 5 min read
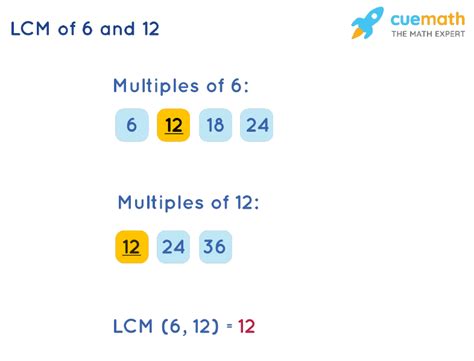
Table of Contents
Finding the Least Common Multiple (LCM) of 12 and 6: A Deep Dive
The least common multiple (LCM) is a fundamental concept in arithmetic and number theory. Understanding how to find the LCM is crucial for various mathematical applications, from simplifying fractions to solving problems involving cycles and periodic events. This article will delve into the calculation of the LCM of 12 and 6, exploring multiple methods and expanding on the underlying mathematical principles. We will also examine real-world applications to solidify understanding and demonstrate the practical relevance of this seemingly simple concept.
Understanding Least Common Multiple (LCM)
Before we tackle the specific problem of finding the LCM of 12 and 6, let's define what the LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. The multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, and so on. The least common multiple is 6.
Method 1: Listing Multiples
One straightforward approach to finding the LCM is by listing the multiples of each number until a common multiple is found. This method is particularly effective for smaller numbers.
Let's apply this method to find the LCM of 12 and 6:
- Multiples of 12: 12, 24, 36, 48, 60, 72...
- Multiples of 6: 6, 12, 18, 24, 30, 36...
By comparing the lists, we can see that the smallest common multiple is 12. Therefore, the LCM(12, 6) = 12.
This method is simple and intuitive, making it ideal for introductory learning. However, it becomes less practical when dealing with larger numbers, as the lists can grow significantly before a common multiple is identified.
Method 2: Prime Factorization
A more efficient and general method for finding the LCM involves prime factorization. This method is particularly useful when working with larger numbers or multiple numbers simultaneously.
Prime factorization is the process of expressing a number as a product of its prime factors. A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers.
Let's find the prime factorization of 12 and 6:
- 12 = 2 x 2 x 3 = 2² x 3
- 6 = 2 x 3
Now, to find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together:
LCM(12, 6) = 2² x 3 = 4 x 3 = 12
This method provides a more systematic and efficient way to calculate the LCM, especially for larger numbers. It avoids the potentially lengthy process of listing multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both integers without leaving a remainder. There's a handy formula that connects the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
Let's use this formula to find the LCM(12, 6). First, we need to find the GCD(12, 6). We can use the Euclidean algorithm or prime factorization to find the GCD.
Using prime factorization:
- 12 = 2² x 3
- 6 = 2 x 3
The common prime factors are 2 and 3. The lowest power of 2 is 2¹, and the lowest power of 3 is 3¹. Therefore, GCD(12, 6) = 2 x 3 = 6.
Now, we can use the formula:
LCM(12, 6) = (12 x 6) / GCD(12, 6) = 72 / 6 = 12
This method demonstrates the elegant relationship between LCM and GCD. It's efficient for numbers where finding the GCD is relatively straightforward.
Real-World Applications of LCM
The LCM finds practical applications in various scenarios:
-
Scheduling: Imagine two buses that leave a station at different intervals. One bus leaves every 12 minutes, and the other leaves every 6 minutes. To find when both buses will depart simultaneously again, we need to find the LCM(12, 6) = 12. Both buses will leave together again in 12 minutes.
-
Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators helps in finding the least common denominator (LCD), simplifying the calculation.
-
Project Management: If two tasks in a project have cycle times of 12 hours and 6 hours, respectively, the LCM helps determine when both tasks will complete a full cycle simultaneously.
-
Gear Ratios: In mechanical engineering, gear ratios often involve LCM to determine the rotational speed of different gears in a system.
-
Music: Musical rhythms and beats frequently involve LCM calculations to determine when different rhythmic patterns will coincide.
Choosing the Right Method
The best method for finding the LCM depends on the numbers involved and your comfort level with different mathematical techniques.
- Listing Multiples: Suitable for small numbers and introductory purposes.
- Prime Factorization: Efficient and generalizable for larger numbers.
- Using GCD: Elegant and efficient if the GCD is readily available.
Understanding these different methods empowers you to choose the most efficient approach for any given problem.
Advanced Concepts and Extensions
The concept of LCM extends beyond two numbers. You can find the LCM of three or more numbers by extending the prime factorization or GCD methods. For example, to find the LCM of 12, 6, and 18, you would find the prime factorization of each number, then take the highest power of each prime factor present:
- 12 = 2² x 3
- 6 = 2 x 3
- 18 = 2 x 3²
LCM(12, 6, 18) = 2² x 3² = 4 x 9 = 36
Conclusion: Mastering LCM for Enhanced Mathematical Fluency
The calculation of the least common multiple, while seemingly simple at first glance, represents a crucial concept with wide-ranging applications across various fields. Mastering the different methods for calculating the LCM – listing multiples, prime factorization, and utilizing the GCD – equips you with essential skills for solving diverse mathematical problems and understanding more complex concepts in number theory. By appreciating the practical relevance of the LCM in real-world scenarios, you can better appreciate its significance and apply it effectively to solve practical problems. The ability to confidently and efficiently calculate the LCM signifies a deeper understanding of fundamental arithmetic principles, enhancing your overall mathematical fluency and problem-solving capabilities.
Latest Posts
Latest Posts
-
7am To 11am Is How Many Hours
Jul 12, 2025
-
If Your 35 What Year Was You Born
Jul 12, 2025
-
How Many Cups Is 1 Pound Of Cheese
Jul 12, 2025
-
30 X 30 Is How Many Square Feet
Jul 12, 2025
-
How Much Does A Half Oz Weigh
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 12 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.