Least Common Multiple Of 15 And 25
Kalali
Mar 09, 2025 · 5 min read
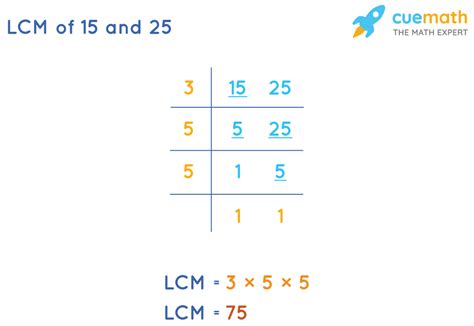
Table of Contents
Finding the Least Common Multiple (LCM) of 15 and 25: A Deep Dive
The least common multiple (LCM) is a fundamental concept in number theory and arithmetic. Understanding how to find the LCM is crucial for various mathematical applications, from simplifying fractions to solving complex algebraic equations. This article will delve into the process of calculating the LCM of 15 and 25, exploring various methods and offering a comprehensive understanding of the underlying principles. We'll move beyond simply finding the answer and explore the broader implications of LCM calculations.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the given numbers as factors. For example, the LCM of 2 and 3 is 6, because 6 is the smallest number divisible by both 2 and 3.
Methods for Finding the LCM of 15 and 25
Several methods exist for calculating the LCM. We'll explore the three most common approaches: listing multiples, prime factorization, and using the greatest common divisor (GCD).
1. Listing Multiples Method
This method involves listing the multiples of each number until a common multiple is found. Let's apply this to 15 and 25:
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, ...
- Multiples of 25: 25, 50, 75, 100, 125, 150, ...
The smallest multiple that appears in both lists is 75. Therefore, the LCM of 15 and 25 is 75.
This method is straightforward for smaller numbers but becomes increasingly cumbersome as the numbers get larger.
2. Prime Factorization Method
This method utilizes the prime factorization of each number. The prime factorization of a number is expressing it as a product of its prime factors.
- Prime factorization of 15: 3 x 5
- Prime factorization of 25: 5 x 5 = 5²
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations:
- The highest power of 3 is 3¹
- The highest power of 5 is 5²
Therefore, the LCM of 15 and 25 is 3¹ x 5² = 3 x 25 = 75.
This method is generally more efficient than listing multiples, especially for larger numbers.
3. Greatest Common Divisor (GCD) Method
This method leverages the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest positive integer that divides both numbers without leaving a remainder. There's a useful formula that connects the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
First, let's find the GCD of 15 and 25 using the Euclidean algorithm:
- Divide the larger number (25) by the smaller number (15): 25 ÷ 15 = 1 with a remainder of 10.
- Replace the larger number with the smaller number (15) and the smaller number with the remainder (10): 15 ÷ 10 = 1 with a remainder of 5.
- Repeat: 10 ÷ 5 = 2 with a remainder of 0.
The last non-zero remainder is the GCD, which is 5.
Now, we can use the formula:
LCM(15, 25) x GCD(15, 25) = 15 x 25 LCM(15, 25) x 5 = 375 LCM(15, 25) = 375 ÷ 5 = 75
This method is also efficient and demonstrates the interconnectedness of LCM and GCD.
Applications of LCM
The concept of LCM finds extensive applications in various fields:
1. Fraction Addition and Subtraction
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial to find a common denominator. This allows us to perform the addition or subtraction effectively.
For example, adding 1/15 and 1/25:
The LCM of 15 and 25 is 75. Therefore:
1/15 + 1/25 = (5/75) + (3/75) = 8/75
2. Scheduling Problems
LCM is frequently used in scheduling problems. Imagine two events that occur at different intervals. The LCM helps determine when both events will coincide. For instance, if event A occurs every 15 days and event B occurs every 25 days, they will coincide every 75 days (the LCM of 15 and 25).
3. Cyclic Patterns
LCM finds applications in analyzing cyclic patterns, whether in physics, engineering or even music. The periodicity of recurring events or processes can be determined by calculating the LCM of their individual cycles.
4. Gear Ratios and Mechanical Systems
In mechanical engineering, the LCM is essential in determining gear ratios and synchronizing rotating components within a system. The design of machinery frequently involves coordinating movements with different periodicities, and the LCM ensures efficient and harmonious operation.
5. Number Theory and Cryptography
LCM plays a vital role in advanced number theory and its applications in cryptography. It forms the basis for various algorithms and calculations essential to ensuring data security and privacy.
Beyond the Basics: Exploring LCM in More Depth
While finding the LCM of 15 and 25 is relatively simple, the underlying principles extend to more complex scenarios. Let's consider some extensions:
- LCM of more than two numbers: The methods described earlier can be extended to find the LCM of three or more numbers. Prime factorization becomes particularly useful in these cases.
- LCM of algebraic expressions: The concept of LCM can be applied to algebraic expressions as well. Finding the LCM of polynomials involves factoring them into their irreducible components.
- Computational complexity: For extremely large numbers, specialized algorithms are needed to compute the LCM efficiently. These algorithms consider the computational complexity of the process to optimize performance.
Conclusion: The Importance of Mastering LCM
Understanding the least common multiple is fundamental to various mathematical and practical applications. The methods discussed in this article—listing multiples, prime factorization, and the GCD method—provide different approaches to calculate the LCM, each with its own strengths and weaknesses. Mastering these methods enables problem-solving across a wide spectrum of disciplines, highlighting the LCM's importance as a core concept in mathematics and its real-world implications. From simplifying fractions to tackling complex scheduling problems, the ability to efficiently find the LCM proves invaluable. The deeper exploration of the LCM's applications beyond simple arithmetic underscores its significance in advanced mathematics and engineering. Remember that practice is key to solidifying your understanding and enhancing your skills in calculating the LCM.
Latest Posts
Latest Posts
-
How Many Months Is A Hundred Days
Jul 18, 2025
-
Mother And I Or Mother And Me
Jul 18, 2025
-
How Many Oz In One Water Bottle
Jul 18, 2025
-
How Many Dimes In A 5 Roll
Jul 18, 2025
-
How Do You Say Basil In Spanish
Jul 18, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 15 And 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.