Least Common Multiple Of 6 5 And 7
Kalali
Jun 13, 2025 · 3 min read
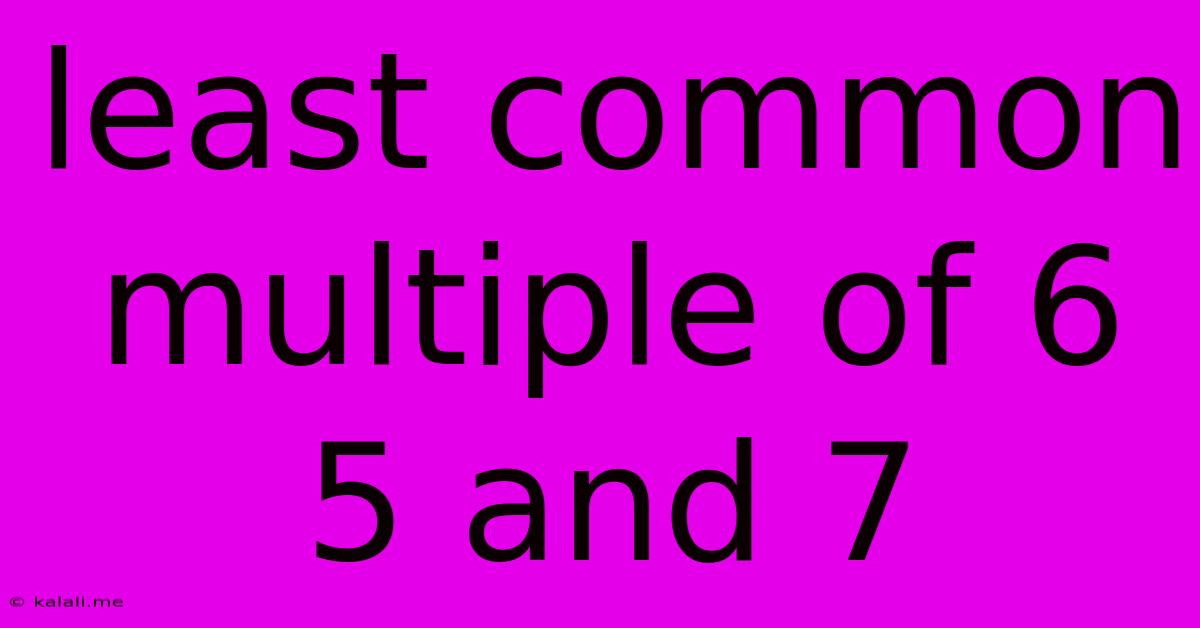
Table of Contents
Finding the Least Common Multiple (LCM) of 6, 5, and 7
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, particularly useful in areas like fractions, scheduling, and even music theory. This article will guide you through calculating the LCM of 6, 5, and 7, explaining the methods and providing a clear understanding of the process. Understanding LCMs can significantly improve your mathematical skills and problem-solving abilities.
What is the Least Common Multiple?
The least common multiple (LCM) is the smallest positive integer that is a multiple of all the numbers in a given set. In simpler terms, it's the smallest number that all the numbers in the set can divide into evenly. This is different from the greatest common divisor (GCD), which is the largest number that divides all the numbers in a set without leaving a remainder.
Methods for Finding the LCM
There are several ways to find the LCM, and we'll explore two common methods: the prime factorization method and the listing multiples method. Both methods will arrive at the same answer, but one might be more efficient depending on the numbers involved.
Method 1: Prime Factorization
This method is generally preferred for larger numbers or sets of numbers. It involves breaking down each number into its prime factors.
-
Find the prime factorization of each number:
- 6 = 2 x 3
- 5 = 5
- 7 = 7
-
Identify the highest power of each prime factor:
- The prime factors are 2, 3, 5, and 7. Each appears only once.
-
Multiply the highest powers together:
- LCM(6, 5, 7) = 2 x 3 x 5 x 7 = 210
Therefore, the least common multiple of 6, 5, and 7 is 210. This means 210 is the smallest number that is divisible by 6, 5, and 7 without leaving a remainder. Understanding prime factorization is crucial for various mathematical operations beyond LCM calculations.
Method 2: Listing Multiples
This method is suitable for smaller numbers. It involves listing the multiples of each number until you find the smallest common multiple.
-
List the multiples of each number:
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96, 102, 108, 114, 120, 126, 132, 138, 144, 150, 156, 162, 168, 174, 180, 186, 192, 198, 204, 210...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115, 120, 125, 130, 135, 140, 145, 150, 155, 160, 165, 170, 175, 180, 185, 190, 195, 200, 205, 210...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133, 140, 147, 154, 161, 168, 175, 182, 189, 196, 203, 210...
-
Find the smallest common multiple: The smallest number that appears in all three lists is 210.
Therefore, using the listing method also confirms that the LCM(6, 5, 7) = 210.
Conclusion:
Both the prime factorization method and the listing multiples method effectively determine the LCM. The prime factorization method is generally more efficient for larger numbers, while the listing method is suitable for smaller numbers where it's easier to visually identify the smallest common multiple. Remember that understanding LCMs is a vital skill in various mathematical applications.
Latest Posts
Latest Posts
-
Which Of The Following Is Not A Protein
Jun 14, 2025
-
Which Of The Following Is Not A Money Market Security
Jun 14, 2025
-
Duvalls Developmental Stages Of The Family
Jun 14, 2025
-
Least Common Multiple Of 27 And 63
Jun 14, 2025
-
1 8 27 64 What Is The Next Number
Jun 14, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 6 5 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.