Lim Sinx X As X Approaches 0
Kalali
Jun 01, 2025 · 3 min read
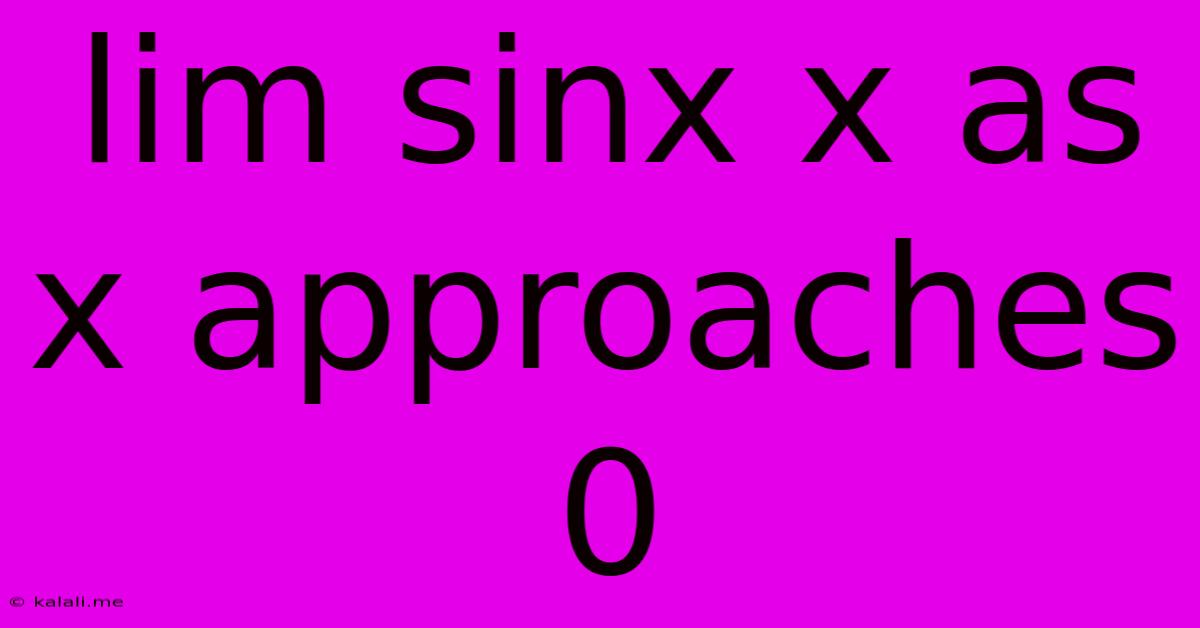
Table of Contents
Evaluating the Limit: lim (sin x / x) as x approaches 0
This article explores the fundamental limit lim (sin x / x) as x approaches 0, a crucial concept in calculus and analysis. Understanding this limit is key to mastering derivatives and other advanced mathematical concepts. We'll delve into its evaluation using both graphical and analytical methods, explaining why this limit is so important and how it's applied.
The limit lim (sin x / x) as x approaches 0 is a cornerstone of calculus, frequently appearing in the derivation of trigonometric derivatives. It's famously equal to 1, a result that may seem counterintuitive at first glance. Let's uncover why.
Understanding the Limit Graphically
Visualizing the function f(x) = sin x / x helps build intuition. While the function is undefined at x = 0, we can examine its behavior as x approaches 0 from both the left and the right. A graph clearly shows that as x gets closer to 0, the value of sin x / x approaches 1. This visual representation provides a strong initial understanding, though a rigorous proof requires analytical methods.
Proving the Limit Analytically using the Squeeze Theorem
A rigorous proof relies on the Squeeze Theorem (also known as the Sandwich Theorem). This theorem states that if we have three functions, f(x), g(x), and h(x), such that f(x) ≤ g(x) ≤ h(x) for all x in an interval around a point c (except possibly at c itself), and lim (x→c) f(x) = lim (x→c) h(x) = L, then lim (x→c) g(x) = L.
To apply the Squeeze Theorem to lim (sin x / x) as x approaches 0, we consider a unit circle. Let x be a small angle (in radians) in the first quadrant. Construct a right-angled triangle within the unit circle, where x is one of the acute angles. Using basic trigonometry and the geometry of the circle, we can establish the following inequalities:
- sin x ≤ x ≤ tan x (for x > 0)
Dividing by sin x (since sin x > 0 for small positive x), we get:
- 1 ≤ x / sin x ≤ 1 / cos x
Inverting the inequality (and flipping the direction of the inequality signs):
- cos x ≤ sin x / x ≤ 1
Now, taking the limit as x approaches 0:
- lim (x→0) cos x = 1
- lim (x→0) 1 = 1
By the Squeeze Theorem, since both limits are 1, we conclude:
- lim (x→0) sin x / x = 1
A similar argument can be made for x approaching 0 from the left (negative values of x), leading to the same conclusion.
Importance and Applications of the Limit
The limit lim (sin x / x) as x approaches 0 is fundamental because it underpins the derivation of the derivative of sin x:
d/dx (sin x) = cos x
This derivative, in turn, is crucial for numerous applications in physics, engineering, and other fields. Understanding this foundational limit allows for a deeper understanding of calculus and its wide-ranging applications in various disciplines, ranging from calculating velocity and acceleration to modeling oscillations and wave phenomena. Its use extends to more advanced mathematical concepts like Taylor series expansions and Fourier analysis.
Conclusion
The evaluation of lim (sin x / x) as x approaches 0, resulting in 1, is not merely a mathematical curiosity. It's a pivotal result with far-reaching consequences. Understanding its proof, both graphically and analytically, provides a solid foundation for further exploration in calculus and related fields. The Squeeze Theorem elegantly demonstrates the limit's value, highlighting the power of analytical techniques in establishing fundamental mathematical truths. This limit's importance underscores its central role in the development of calculus and its widespread applications.
Latest Posts
Latest Posts
-
What Part Of Speech Is As
Jun 03, 2025
-
How Can You Tell If The Propane Tank Is Empty
Jun 03, 2025
-
Size Of Toothpaste For Carry On
Jun 03, 2025
-
How To Pluralize A Name Ending In S
Jun 03, 2025
-
Does Dawn Dish Soap Kill Grass
Jun 03, 2025
Related Post
Thank you for visiting our website which covers about Lim Sinx X As X Approaches 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.