Lines Of Symmetry Of A Hexagon
Kalali
Mar 31, 2025 · 6 min read
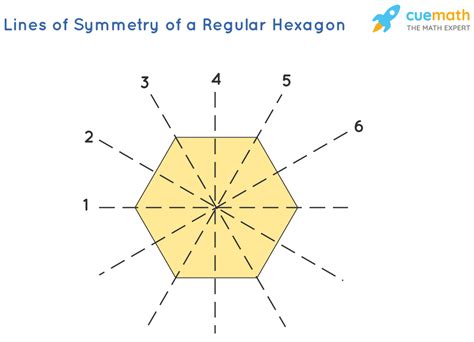
Table of Contents
Lines of Symmetry of a Hexagon: A Comprehensive Guide
Understanding lines of symmetry is crucial in geometry, offering insights into the inherent structure and properties of shapes. This comprehensive guide delves deep into the lines of symmetry of a hexagon, exploring different types of hexagons and the mathematical principles behind their symmetrical properties. We'll cover regular hexagons, irregular hexagons, and even explore the concept of rotational symmetry as it relates to hexagons. By the end, you'll have a robust understanding of this fascinating geometric concept.
What is a Line of Symmetry?
Before diving into the intricacies of hexagons, let's establish a firm understanding of the fundamental concept: a line of symmetry. A line of symmetry, also known as a line of reflection, is a line that divides a shape into two identical halves. If you were to fold the shape along this line, the two halves would perfectly overlap. Shapes can have multiple lines of symmetry, or none at all.
The Regular Hexagon: A Paragon of Symmetry
The most common type of hexagon we encounter is the regular hexagon. This is a hexagon with all sides of equal length and all interior angles equal (each measuring 120 degrees). This uniformity leads to a remarkable degree of symmetry.
How Many Lines of Symmetry Does a Regular Hexagon Have?
A regular hexagon possesses six lines of symmetry. These lines can be categorized into two types:
-
Three lines of symmetry connecting opposite vertices: These lines run directly from one vertex (corner) to the opposite vertex. Imagine drawing a line from the top vertex to the bottom vertex, then another from the top-right to the bottom-left, and finally from the top-left to the bottom-right. These three lines perfectly bisect the hexagon.
-
Three lines of symmetry connecting midpoints of opposite sides: These lines connect the midpoints of two parallel sides. Since a regular hexagon has three pairs of parallel sides, you'll find three lines of symmetry of this type.
Visualizing the Lines of Symmetry: Imagine a regular hexagon drawn on a piece of paper. You can easily fold it along each of these six lines, and the two halves will perfectly overlap, confirming their symmetrical nature.
Mathematical Proof of Symmetry
The existence of these six lines of symmetry is not just an observation; it's a direct consequence of the regular hexagon's inherent properties. The equal side lengths and angles create a perfectly balanced structure that inherently supports this multiple symmetry. This can be formally proven using coordinate geometry and transformation matrices, though this goes beyond the scope of this introductory guide.
Irregular Hexagons: A Less Symmetrical Affair
Unlike regular hexagons, irregular hexagons have sides and angles of varying lengths and measures. This lack of uniformity significantly impacts the number of lines of symmetry.
Lines of Symmetry in Irregular Hexagons
An irregular hexagon may have:
-
Zero lines of symmetry: Most irregular hexagons lack any lines of symmetry. The asymmetrical arrangement of their sides and angles prevents any such lines from existing.
-
One or more lines of symmetry (rare): In rare cases, an irregular hexagon might possess one or more lines of symmetry. This would require a specific and symmetrical arrangement of its sides and angles, which is quite uncommon. Even with one line of symmetry, it would not have the six lines of symmetry a regular hexagon enjoys.
Identifying lines of symmetry in irregular hexagons requires careful observation and potentially the use of geometrical tools like rulers and protractors to verify if a fold will result in a perfect overlap of the two halves.
Rotational Symmetry: A Related Concept
While we've focused primarily on lines of symmetry, it's important to acknowledge the concept of rotational symmetry. This refers to a shape's ability to remain unchanged after rotation around a central point.
Rotational Symmetry in Hexagons
A regular hexagon has rotational symmetry of order 6. This means it can be rotated six times (by 60-degree increments) around its center point and still look identical. Each of these rotations corresponds to one of the lines of symmetry.
Irregular hexagons may have rotational symmetry of order 1 (meaning no rotational symmetry), or order 2 (180 degree rotational symmetry) in rare cases with specific arrangements of its sides and angles.
Practical Applications of Hexagonal Symmetry
Understanding lines of symmetry in hexagons isn't just a purely academic exercise; it has several practical applications:
-
Design and Architecture: Hexagonal patterns are commonly used in architecture and design due to their inherent stability and aesthetic appeal. The symmetry of hexagons makes them suitable for creating visually appealing and structurally sound designs. Think of honeycomb structures in nature, or tiled floors.
-
Engineering: Hexagonal shapes are used in engineering applications where strength and stability are essential. The symmetrical distribution of forces in a hexagon makes it suitable for various engineering components.
-
Art and Crafts: Hexagonal patterns are prevalent in various art forms, including mosaics, tessellations, and quilting. The symmetrical nature of hexagons offers artists a versatile tool for creating visually appealing patterns.
Beyond the Basics: Exploring More Complex Scenarios
The concepts discussed so far provide a solid foundation for understanding the lines of symmetry in hexagons. However, considerations can extend beyond the basic regular and irregular cases.
-
Concave Hexagons: Hexagons can be concave, meaning they have at least one interior angle greater than 180 degrees. Concave hexagons might possess fewer lines of symmetry than their convex counterparts, or even none at all. The presence of a line of symmetry depends entirely on the specific shape of the concave hexagon.
-
Three-Dimensional Hexagons: The concept of lines of symmetry extends to three-dimensional shapes as well. A hexagonal prism, for example, exhibits more complex symmetry properties due to its added dimension.
-
Symmetry in Fractal Hexagons: In fractal geometry, hexagons can form complex, self-similar patterns. Understanding the symmetry within these patterns requires a deeper dive into fractal mathematics.
Conclusion: Symmetry Unveiled
The exploration of lines of symmetry in hexagons reveals a fascinating interplay between geometry and symmetry. While regular hexagons boast a remarkable six lines of symmetry, irregular hexagons may possess fewer or none. Understanding these distinctions, along with the related concept of rotational symmetry, offers a deeper appreciation for the inherent structure and beauty of these shapes, extending into diverse applications across numerous fields. This knowledge provides a powerful foundation for anyone interested in geometry, design, or any field where understanding symmetry is crucial. Further exploration into the more complex scenarios mentioned above can lead to even more fascinating insights into the world of hexagonal symmetry.
Latest Posts
Latest Posts
-
How Much Is 48 Cm In Inches
Apr 01, 2025
-
What Is 3 Out Of 5
Apr 01, 2025
-
What Is The Percent Of 8 12
Apr 01, 2025
-
Gravitational Force Of Earth And Sun
Apr 01, 2025
-
How Many Quarts In 12 Cups
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Lines Of Symmetry Of A Hexagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
