Log Ab Log A Log B
Kalali
May 30, 2025 · 3 min read
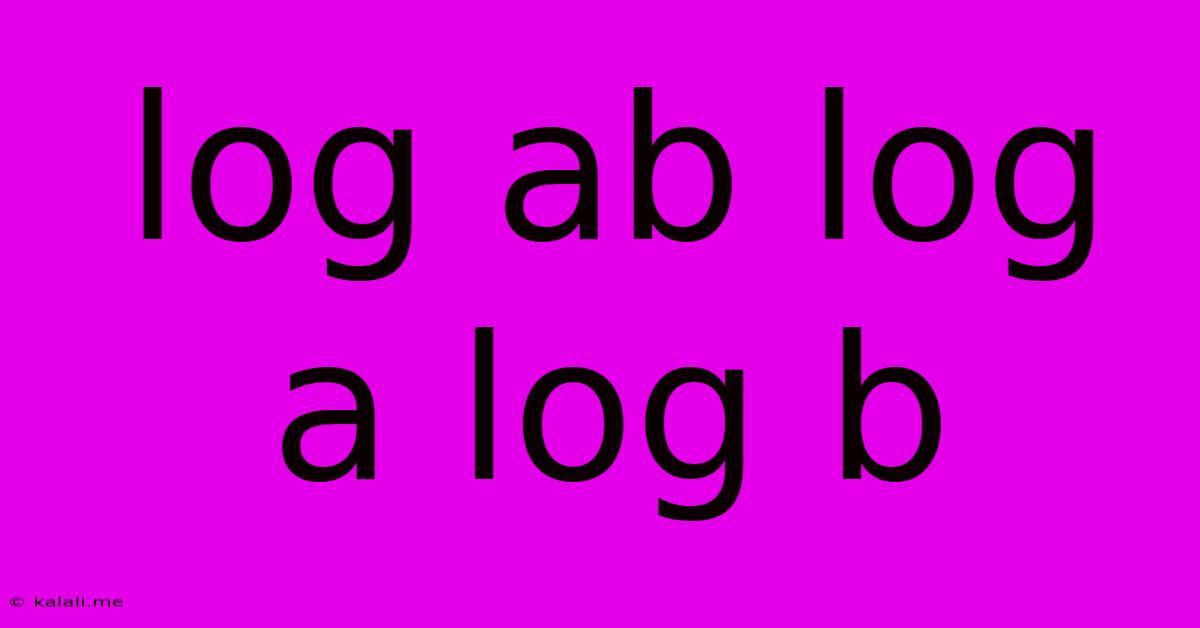
Table of Contents
Exploring the Logarithmic Identity: logₐb logₐb
This article delves into the intriguing expression logₐb logₐb, exploring its properties, limitations, and potential interpretations. While this specific notation might not represent a standard logarithmic identity, we can analyze it by breaking down the expression and exploring related logarithmic rules. Understanding the behavior of logarithms is crucial for various fields, from mathematics and computer science to physics and finance. This exploration aims to provide a clear understanding and potentially uncover some interesting mathematical relationships.
Understanding the Components: Logarithms and Their Bases
Before diving into the expression, let's revisit the fundamental concept of logarithms. The logarithm of a number x to a base a (written as logₐx) is the exponent to which a must be raised to produce x. In simpler terms:
- a<sup>logₐx</sup> = x
The base 'a' is crucial; a different base will result in a different logarithmic value for the same number x. Common bases include 10 (common logarithm), e (natural logarithm, often denoted as ln), and 2 (binary logarithm).
Interpreting logₐb logₐb:
The expression logₐb logₐb presents a nested logarithmic structure. It can be interpreted in two primary ways, both highlighting important aspects of logarithmic behavior:
1. As a Repeated Application:
This interpretation views the expression as a sequential application of the logarithm function. First, logₐb is calculated, producing a numerical result. This result is then used as the input for a second logarithmic operation, logₐ(result). The result will vary considerably depending on the values of 'a' and 'b', showcasing the sensitivity of logarithms to changes in the base and argument. The calculation is straightforward, but the final outcome isn't readily simplified into a concise, universally applicable formula.
2. As a Potential for Misinterpretation:
It's important to emphasize that logₐb logₐb is not equivalent to any standard logarithmic identity such as the product rule (logₐ(xy) = logₐx + logₐy) or the power rule (logₐ(x<sup>y</sup>) = y logₐx). The absence of an operator (like +, -, *, or /) between the two logₐb terms prevents any direct simplification using conventional logarithmic rules. The expression is simply the square of the logarithm of b to base a.
Practical Considerations and Limitations:
- Domain Restrictions: The base 'a' must be positive and not equal to 1. The argument 'b' must also be positive. Violating these conditions will result in undefined or complex logarithmic values.
- Numerical Computation: While there isn't a closed-form simplification, the expression can be readily evaluated numerically using a calculator or programming language for specific values of 'a' and 'b'.
- No General Simplification: Despite the seemingly simple structure, there’s no general algebraic simplification that reduces
logₐb logₐbto a more elementary form applicable for all 'a' and 'b'.
Conclusion:
The expression logₐb logₐb, while not representing a standard logarithmic identity, provides a valuable exercise in understanding logarithmic operations. Its analysis demonstrates the importance of proper notation and emphasizes that seemingly simple expressions can yield complex results dependent on the specific values involved. Remember, meticulous attention to the base and argument is crucial when working with logarithms. Through numerical computation and a clear understanding of the underlying logarithmic principles, we can effectively explore and interpret expressions such as this one.
Latest Posts
Latest Posts
-
How Did Dumbledore And Rab Know About The Horcrux Place
May 31, 2025
-
Does The Sun Amplify Radio Waves
May 31, 2025
-
Show Grants For All Users In Mysql
May 31, 2025
-
How To Make Soda Flat Instantly
May 31, 2025
-
How To Enable The User In Sql Server
May 31, 2025
Related Post
Thank you for visiting our website which covers about Log Ab Log A Log B . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.