Lowest Common Factor Of 3 And 5
Kalali
Mar 31, 2025 · 5 min read
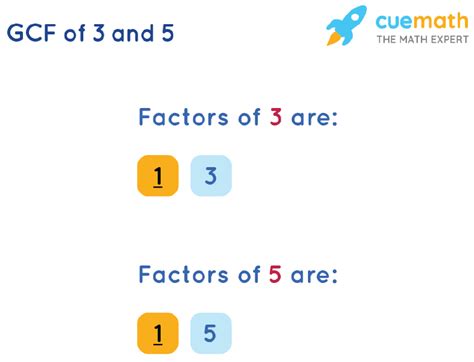
Table of Contents
Unveiling the Mysteries of the Lowest Common Factor: A Deep Dive into the LCM of 3 and 5
Finding the lowest common factor (LCF) of two numbers might seem like a simple arithmetic task, suitable only for elementary school students. However, understanding the underlying concepts and exploring the broader implications of LCFs opens up a fascinating world of mathematical principles with practical applications across various fields. This comprehensive guide delves into the LCF of 3 and 5, explaining the process, exploring related concepts like the greatest common divisor (GCD), and demonstrating its relevance in real-world scenarios.
Understanding the Concept of Lowest Common Factor (LCF)
Before we jump into the specifics of the LCF of 3 and 5, let's solidify our understanding of the term itself. The lowest common factor (LCF), also known as the greatest common divisor (GCD) or highest common factor (HCF), is the largest number that divides exactly into two or more numbers without leaving a remainder. It's crucial to distinguish this from the least common multiple (LCM), which is the smallest number that is a multiple of two or more numbers. While seemingly similar, these concepts are distinct and serve different purposes.
In simpler terms, the LCF represents the largest shared factor among a set of numbers. For instance, the LCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
Calculating the LCF of 3 and 5
Now, let's focus on the specific numbers we're interested in: 3 and 5. These numbers are both prime numbers, meaning their only factors are 1 and themselves. This significantly simplifies the process of finding their LCF.
Since 3 and 5 have no common factors other than 1, their LCF is 1.
Therefore, the lowest common factor (LCF) of 3 and 5 is 1.
Exploring Prime Numbers and Their Significance
The fact that both 3 and 5 are prime numbers is crucial to understanding their LCF. Prime numbers are the building blocks of all other numbers, and their properties are fundamental to many mathematical concepts. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, and so on.
Understanding prime numbers is essential for various mathematical operations, including factorization, cryptography, and number theory. The distribution and properties of prime numbers have been a source of fascination and research for mathematicians for centuries. The Prime Number Theorem, for example, provides an approximation of the number of primes less than a given number.
Connecting LCF and LCM: A Complementary Relationship
While we've focused on the LCF of 3 and 5, it's helpful to understand its relationship with the LCM. The LCF and LCM are inversely proportional. The product of the LCF and LCM of two numbers is always equal to the product of the two numbers themselves.
In the case of 3 and 5:
- LCF(3, 5) = 1
- LCM(3, 5) = 15
- Product of the numbers: 3 * 5 = 15
As you can see, the product of the LCF and LCM (1 * 15) equals the product of the numbers (15). This relationship holds true for any pair of integers. This complementary relationship provides a convenient way to calculate the LCM if the LCF is already known, and vice versa.
Methods for Finding the LCF (GCD) of Larger Numbers
While finding the LCF of 3 and 5 is straightforward, determining the LCF of larger numbers requires more sophisticated techniques. Two common methods are:
1. Prime Factorization:
This method involves breaking down each number into its prime factors. The LCF is then found by identifying the common prime factors and multiplying them together. For example:
Let's find the LCF of 24 and 36:
- Prime factorization of 24: 2³ * 3
- Prime factorization of 36: 2² * 3²
The common prime factors are 2² and 3. Therefore, the LCF(24, 36) = 2² * 3 = 12.
2. Euclidean Algorithm:
This is an efficient algorithm for finding the GCD of two numbers. It involves repeatedly applying the division algorithm until the remainder is zero. The last non-zero remainder is the GCD. Let's illustrate with an example:
Find the LCF of 48 and 18:
- Divide 48 by 18: 48 = 2 * 18 + 12
- Divide 18 by the remainder 12: 18 = 1 * 12 + 6
- Divide 12 by the remainder 6: 12 = 2 * 6 + 0
Since the last non-zero remainder is 6, the LCF(48, 18) = 6.
Applications of LCF in Real-World Scenarios
While the concept of LCF might seem purely theoretical, it finds practical applications in various fields:
- Geometry: LCF plays a crucial role in simplifying fractions and ratios in geometric problems.
- Music Theory: Understanding the LCF helps in determining the relationships between different musical notes and intervals.
- Computer Science: The LCF is used in algorithms for data compression and cryptography.
- Engineering: LCF is applied in simplifying ratios and proportions in engineering designs.
Conclusion: The Importance of Understanding Fundamental Concepts
The seemingly simple task of finding the lowest common factor of 3 and 5 reveals a deeper understanding of fundamental mathematical concepts such as prime numbers, factorization, and the relationship between LCF and LCM. Mastering these concepts is essential for tackling more complex mathematical problems and for applying mathematical principles to real-world scenarios across various fields. The exploration of LCF extends beyond a simple arithmetic calculation, offering a gateway to a broader appreciation of the elegance and power of mathematics. The seemingly simple example of 3 and 5, with their LCF of 1, serves as a powerful illustration of the fundamental building blocks of number theory and its widespread applications. By understanding this seemingly simple concept, we unlock a deeper appreciation for the intricacies and practical utility of mathematics.
Latest Posts
Latest Posts
-
What Is 400 Fahrenheit In Centigrade
Apr 02, 2025
-
50 Oz Is How Many Liters
Apr 02, 2025
-
How Many Feet Is 109 Inches
Apr 02, 2025
-
What Is In Both Eukaryotic And Prokaryotic Cells
Apr 02, 2025
-
What Is A 60 Out Of 100
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Lowest Common Factor Of 3 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
