Maclaurin Series For 1 1 X 2
Kalali
May 24, 2025 · 3 min read
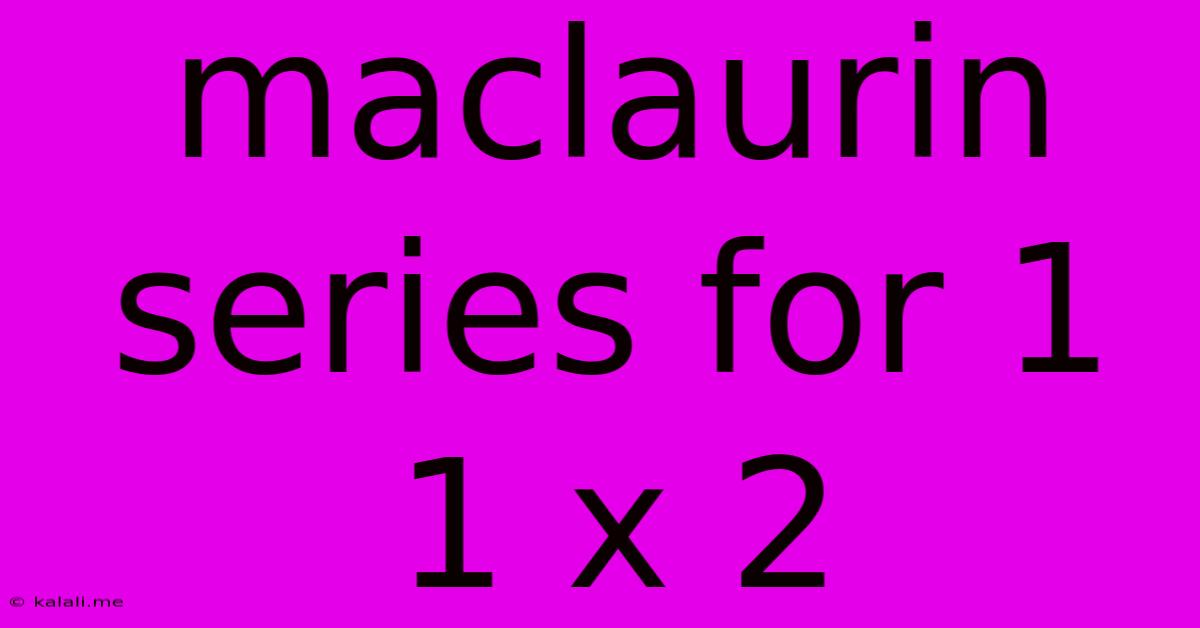
Table of Contents
Maclaurin Series for 1/(1 + x²)
The Maclaurin series is a powerful tool in calculus for representing functions as infinite sums of power terms. It's essentially a special case of the Taylor series, centered at x = 0. This article will explore the derivation and application of the Maclaurin series for the function f(x) = 1/(1 + x²). Understanding this series offers insights into approximating complex functions and solving various mathematical problems.
This article will cover:
- Understanding the Geometric Series
- Deriving the Maclaurin Series for 1/(1 + x²)
- Radius and Interval of Convergence
- Applications of the Maclaurin Series
Understanding the Geometric Series
Before diving into the Maclaurin series, it's crucial to understand the geometric series formula:
1 + x + x² + x³ + ... = 1/(1 - x), |x| < 1
This formula states that the sum of an infinite geometric series converges to 1/(1 - x) as long as the absolute value of x is less than 1. This restriction is vital for the convergence of the series. If |x| ≥ 1, the series diverges.
Deriving the Maclaurin Series for 1/(1 + x²)
To find the Maclaurin series for 1/(1 + x²), we can cleverly manipulate the geometric series formula. Notice that 1/(1 + x²) can be rewritten as 1/(1 - (-x²)). Now, we can directly substitute (-x²) for x in the geometric series formula:
1 + (-x²) + (-x²)² + (-x²)³ + ... = 1/(1 - (-x²)) = 1/(1 + x²)
Simplifying the terms, we get:
1 - x² + x⁴ - x⁶ + x⁸ - ... = 1/(1 + x²)
This is the Maclaurin series for 1/(1 + x²). Each term is obtained by raising (-x²) to successive powers.
Radius and Interval of Convergence
The convergence of the Maclaurin series is dependent on the absolute value of (-x²). For the geometric series to converge, we need |(-x²)| < 1. Since x² is always non-negative, this simplifies to |x²| < 1, which further simplifies to |x| < 1.
Therefore, the radius of convergence is 1. The interval of convergence is -1 < x < 1. At the endpoints x = 1 and x = -1, the series does not converge.
Applications of the Maclaurin Series
The Maclaurin series for 1/(1 + x²) has several applications, including:
-
Approximating values: For values of x within the interval of convergence, the series provides an accurate approximation of 1/(1 + x²). The more terms included, the more precise the approximation becomes.
-
Solving differential equations: The series can be used to find solutions to certain differential equations.
-
Integration: Integrating the Maclaurin series term by term can sometimes lead to simpler expressions, enabling the calculation of otherwise intractable integrals. This is particularly useful when dealing with integrals involving 1/(1 + x²).
-
Understanding trigonometric functions: This series is closely related to the Maclaurin series for arctan(x), as the derivative of arctan(x) is 1/(1 + x²). This connection reveals a fascinating link between algebraic series and trigonometric functions.
In conclusion, the Maclaurin series for 1/(1 + x²) provides a powerful tool for approximating the function, solving mathematical problems, and exploring relationships between different areas of mathematics. Understanding its derivation and convergence properties is crucial for effectively applying this valuable series.
Latest Posts
Latest Posts
-
He Will Give You The Desires Of Your Heart
May 24, 2025
-
How Hot Does A Dishwasher Get
May 24, 2025
-
Examples Of A Gas Dissolved In A Gas
May 24, 2025
-
How To Dispose Of Muriatic Acid
May 24, 2025
-
I Have Brought Peace Freedom Justice And Security
May 24, 2025
Related Post
Thank you for visiting our website which covers about Maclaurin Series For 1 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.