Maclaurin Series For 1 X 2
Kalali
May 29, 2025 · 3 min read
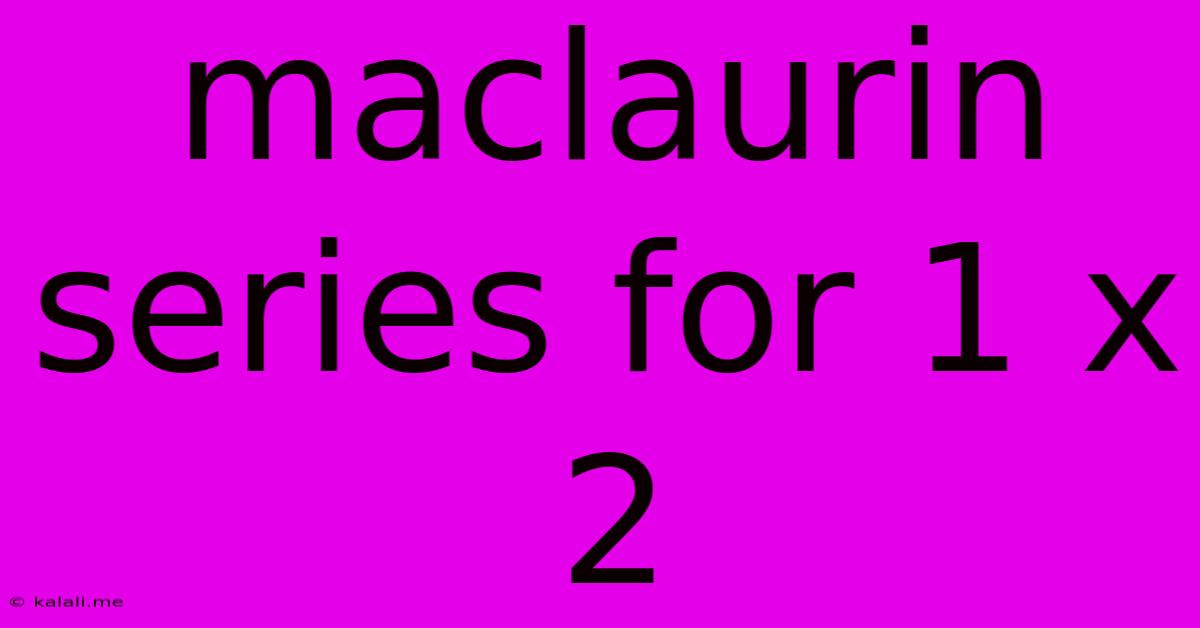
Table of Contents
Maclaurin Series for 1/(1+x)²
The Maclaurin series, a special case of the Taylor series expansion, provides a way to represent a function as an infinite sum of terms. This allows us to approximate the function's value at a specific point using a polynomial. This article will delve into deriving the Maclaurin series for the function f(x) = 1/(1+x)², exploring its derivation and applications. Understanding this series is crucial for various applications in calculus, physics, and engineering.
Understanding the Maclaurin Series
The Maclaurin series of a function f(x) is given by:
f(x) = Σ (f⁽ⁿ⁾(0)/n!) * xⁿ, where n ranges from 0 to ∞.
This formula represents the function as a sum of its derivatives evaluated at x=0, multiplied by corresponding powers of x and factorial terms. The key to finding the Maclaurin series lies in calculating these derivatives.
Deriving the Maclaurin Series for 1/(1+x)²
We start with the well-known geometric series:
1/(1+x) = Σ (-x)ⁿ, for |x| < 1. (This is a fundamental series often used as a building block for deriving other series).
Now, we need to find the series for 1/(1+x)². We can achieve this by differentiating the geometric series term by term:
d/dx [1/(1+x)] = d/dx [Σ (-x)ⁿ]
This gives us:
-1/(1+x)² = Σ n*(-x)ⁿ⁻¹ *(-1) (Remember the chain rule and power rule for differentiation).
Simplifying, we obtain:
1/(1+x)² = Σ n*xⁿ⁻¹ , for |x| < 1.
This is the Maclaurin series for 1/(1+x)². Let's write out the first few terms to illustrate:
1/(1+x)² = 1 - 2x + 3x² - 4x³ + 5x⁴ - ...
Applications of the Maclaurin Series for 1/(1+x)²
This series finds applications in several areas:
-
Approximating function values: For values of x close to 0, the series provides an accurate approximation of 1/(1+x)². The more terms included, the better the approximation within the radius of convergence.
-
Solving differential equations: Maclaurin series can be used to find approximate solutions to differential equations, especially those that don't have closed-form solutions.
-
Probability and Statistics: This series can appear in various probability distributions and their moment-generating functions.
-
Physics and Engineering: The series finds its use in approximating physical phenomena described by functions similar to 1/(1+x)².
Limitations and Radius of Convergence
It's crucial to remember that the Maclaurin series only converges for |x| < 1. Outside this interval, the series diverges and doesn't represent the function. This radius of convergence is a key aspect to consider when applying the series.
Conclusion
The Maclaurin series for 1/(1+x)² offers a powerful tool for approximating the function and solving various problems in mathematics, science, and engineering. By understanding its derivation and limitations, one can effectively utilize this series within its radius of convergence to obtain accurate approximations and insights into the behaviour of the function. Remember to always check the radius of convergence before applying the series to any specific value of x.
Latest Posts
Latest Posts
-
What Does It Mean To Goose Someone
May 31, 2025
-
Wire Size For 60 Amp 220v
May 31, 2025
-
Why Do Blacks Have Such Big Lips
May 31, 2025
-
How Much To Tip Shuttle Driver
May 31, 2025
-
How To Get Rid Of Silverfish Bug
May 31, 2025
Related Post
Thank you for visiting our website which covers about Maclaurin Series For 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.