Percentage Of 3 Out Of 5
Kalali
Mar 08, 2025 · 5 min read
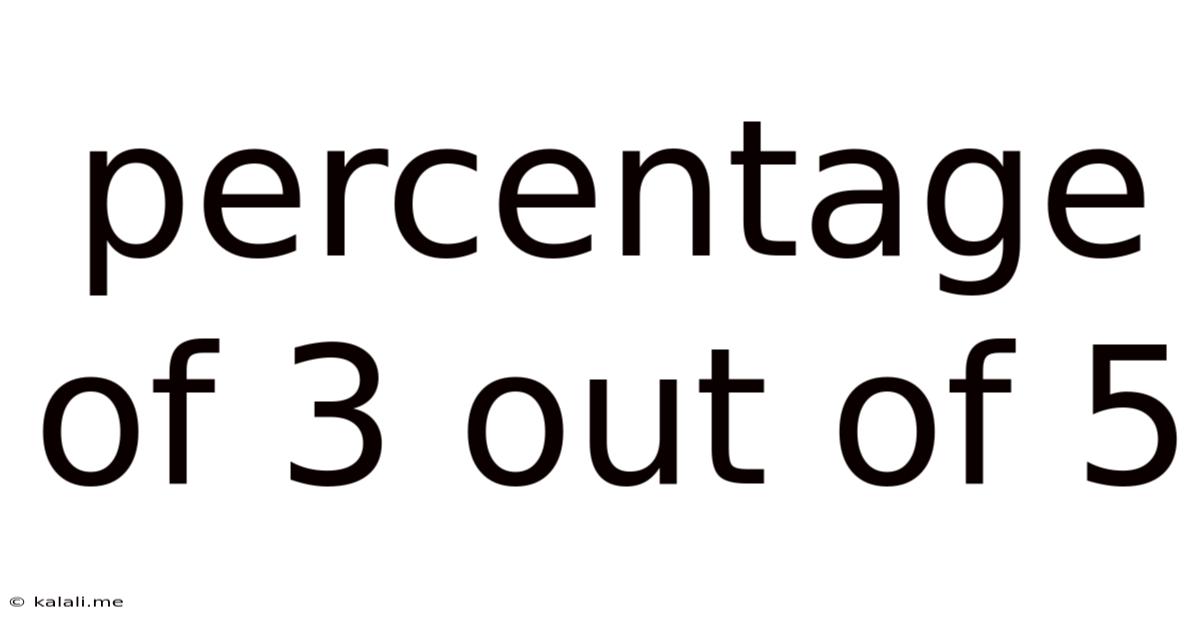
Table of Contents
Understanding the Percentage of 3 out of 5: A Comprehensive Guide
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting and shopping to complex scientific research and financial analysis. Understanding how to calculate percentages accurately and efficiently is therefore crucial. This article will delve deep into understanding the percentage of 3 out of 5, providing a comprehensive explanation, practical examples, and exploring related concepts to build a strong foundational understanding.
What Does "Percentage" Mean?
Before we dive into the specifics of 3 out of 5, let's solidify our understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ("per" meaning "for every" and "cent" meaning "hundred"). So, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or one-half.
Calculating the Percentage of 3 out of 5
Now, let's tackle the core question: what percentage is 3 out of 5? To calculate this, we follow a straightforward three-step process:
Step 1: Formulate the Fraction:
First, represent the given information as a fraction. In this case, 3 out of 5 is written as 3/5.
Step 2: Convert the Fraction to a Decimal:
Next, convert the fraction into a decimal. To do this, simply divide the numerator (the top number) by the denominator (the bottom number):
3 ÷ 5 = 0.6
Step 3: Convert the Decimal to a Percentage:
Finally, convert the decimal to a percentage by multiplying it by 100 and adding the "%" symbol:
0.6 x 100 = 60%
Therefore, 3 out of 5 is equal to 60%.
Practical Applications: Real-World Examples
The concept of calculating percentages, and specifically understanding the percentage of 3 out of 5, has numerous practical applications in various fields. Let's explore some examples:
1. Academic Performance:
Imagine a student taking a 5-question quiz and answering 3 questions correctly. Their score would be 60% (3/5 x 100). This percentage is a common way to represent academic performance and progress.
2. Sales and Marketing:
Suppose a salesperson has 5 potential clients and successfully closes deals with 3 of them. Their conversion rate is 60%. This metric is essential for tracking sales performance and optimizing marketing strategies.
3. Manufacturing and Quality Control:
In a manufacturing process, if 5 items are produced, and 3 meet quality standards, the yield rate is 60%. This is a crucial aspect of quality control and helps identify potential areas for improvement.
4. Survey Results:
If a survey is conducted with 5 participants, and 3 respondents answer "yes" to a specific question, the response rate for "yes" is 60%. This assists in analyzing survey data and drawing relevant conclusions.
5. Financial Investments:
Let's say you invest in 5 different stocks, and 3 of them yield profits. Your successful investment rate is 60%. This type of analysis is crucial for portfolio management.
Beyond 3 out of 5: Understanding Percentage Calculations More Broadly
The process for calculating percentages isn't limited to just 3 out of 5. The same fundamental steps can be applied to any fraction:
- Formulate the Fraction: Express the given numbers as a fraction (part/whole).
- Convert to Decimal: Divide the numerator by the denominator.
- Convert to Percentage: Multiply the decimal by 100 and add the "%" symbol.
Common Percentage Calculations and their Applications:
Here are some other common percentage calculations and where you might encounter them:
- 20%: Often used in discounts, sales, and tax rates. For example, a 20% discount on a $100 item means a saving of $20.
- 50%: Represents one-half, commonly used to express equal proportions or halves.
- 75%: Represents three-quarters, often used in progress indicators or completion rates.
- 100%: Represents the whole or entirety of something.
- Calculating Percentage Increase/Decrease: This involves finding the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] x 100. This is crucial for tracking growth in sales, profits, or other metrics.
- Calculating Percentage of a Number: To find the percentage of a number, multiply the number by the percentage (expressed as a decimal). For example, 25% of 200 is 200 x 0.25 = 50.
Advanced Percentage Concepts
Beyond basic calculations, understanding advanced percentage concepts can be immensely helpful:
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest from previous periods. Understanding compound interest is vital for long-term financial planning and investment strategies.
- Percentage Points vs. Percentages: It's crucial to distinguish between these two terms. A percentage point refers to an absolute change in percentage values, while a percentage refers to a relative change. For example, an increase from 10% to 15% is a 5 percentage point increase, but a 50% increase relative to the original 10%.
- Weighted Averages: These averages take into account the relative importance or weight of different values. This is used in various scenarios, like calculating grade point averages (GPAs) where different courses may have different credit weights.
Mastering Percentages: Tips and Tricks
To master percentage calculations, consider these helpful tips:
- Practice Regularly: Consistent practice is key to building proficiency. Try solving various percentage problems to solidify your understanding.
- Use Online Calculators (for verification only): While calculators are convenient for quick calculations, it's crucial to understand the underlying principles before relying solely on them. Use them primarily for verification after manually solving a problem.
- Learn Mental Math Techniques: Practicing mental math shortcuts can improve your speed and accuracy in percentage calculations.
- Break Down Complex Problems: If you encounter complex percentage problems, break them down into smaller, manageable steps.
- Understand the Context: Always consider the context of the problem to ensure your calculations are relevant and accurate.
Conclusion: The Power of Percentage Understanding
Understanding the percentage of 3 out of 5, and percentage calculations in general, is a foundational skill applicable across many fields. From daily life decisions to complex financial analyses, mastering percentages empowers you to interpret data, make informed decisions, and solve problems more effectively. By mastering these concepts and utilizing the provided tips and tricks, you'll be well-equipped to confidently tackle any percentage-related challenge you encounter. Remember that consistent practice and a clear understanding of the underlying principles are the keys to success.
Latest Posts
Latest Posts
-
How Many Tbsp In A Dry Ounce
Jul 02, 2025
-
How Do You Say Grandparents In Spanish
Jul 02, 2025
-
How Many Numbers Are Between 48 To 24
Jul 02, 2025
-
How Many Positions Are There In Sex
Jul 02, 2025
-
How Many Minutes Are In 10 Miles
Jul 02, 2025
Related Post
Thank you for visiting our website which covers about Percentage Of 3 Out Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.