Percentage Of 5 Out Of 8
Kalali
Mar 11, 2025 · 5 min read
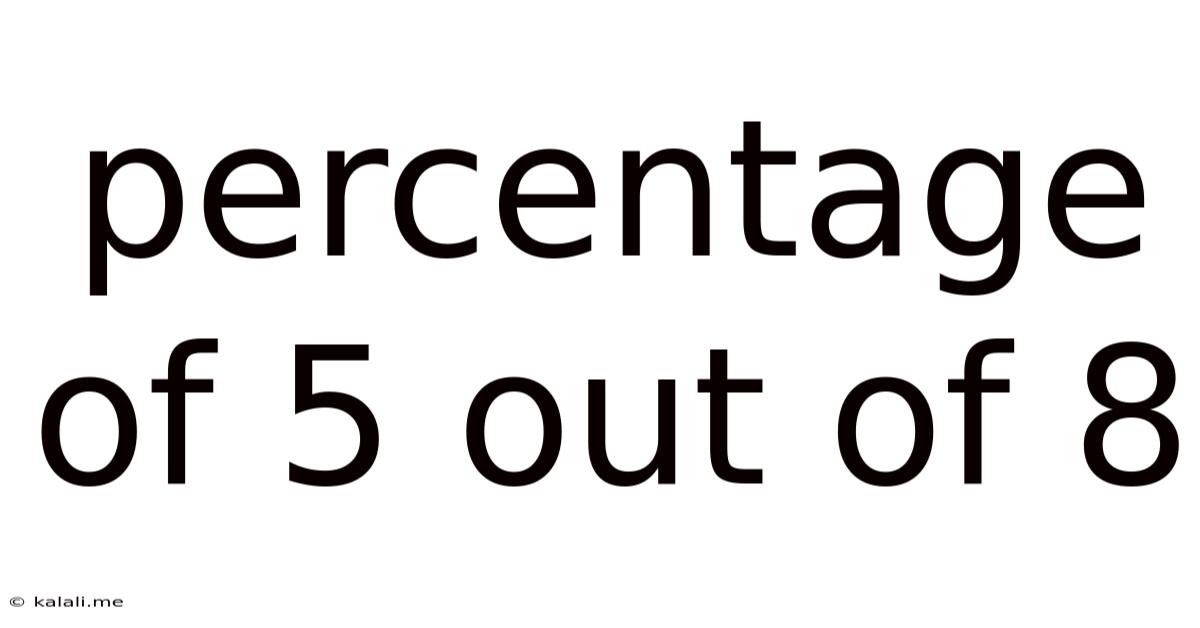
Table of Contents
Decoding Percentages: A Deep Dive into "5 out of 8" and Beyond
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday finances to complex scientific calculations. This article delves into the seemingly simple question of "What percentage is 5 out of 8?" and expands upon the core concepts, providing practical applications and tackling common misconceptions along the way.
What Percentage is 5 out of 8? The Calculation
The calculation of a percentage is straightforward. We need to find what fraction 5 out of 8 represents and then convert that fraction into a percentage.
1. Express as a Fraction: The phrase "5 out of 8" directly translates into the fraction 5/8.
2. Convert to Decimal: To convert a fraction to a decimal, we divide the numerator (5) by the denominator (8): 5 ÷ 8 = 0.625
3. Convert to Percentage: To convert a decimal to a percentage, we multiply by 100: 0.625 × 100 = 62.5%
Therefore, 5 out of 8 is 62.5%.
Beyond the Basic Calculation: Understanding Percentages
While calculating "5 out of 8" is straightforward, a deeper understanding of percentages allows for more complex applications and problem-solving.
Understanding Fractions: The foundation of percentage calculations lies in the understanding of fractions. A fraction represents a part of a whole. In our example, 5/8 means 5 parts out of a total of 8 parts. The numerator (top number) represents the part, and the denominator (bottom number) represents the whole.
Decimal Equivalents: Decimal numbers are another way of representing fractions. They are particularly useful when working with percentages because percentages are inherently based on the decimal system (hundredths).
Percentage as a Ratio: A percentage can also be viewed as a ratio expressed as a fraction of 100. For example, 62.5% can be written as 62.5/100. This perspective can be very helpful in understanding proportional relationships.
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in many real-world scenarios:
1. Finance and Budgeting: Calculating interest rates, discounts, taxes, and profit margins all rely heavily on percentage calculations. Understanding percentages is essential for making informed financial decisions. For example, if a store offers a 20% discount on an item, you need to calculate the final price by subtracting 20% of the original price.
2. Statistics and Data Analysis: Percentages are frequently used to represent proportions within datasets. This is used to illustrate trends, make comparisons, and draw conclusions. For instance, in survey results, percentages are often used to express the proportion of respondents who answered in a specific way.
3. Science and Engineering: Percentages are frequently used in scientific experiments and engineering applications to express the degree of change, efficiency, or accuracy. For example, calculating the percentage error in a measurement is common in experimental sciences.
4. Everyday Life: Calculating tips in restaurants, figuring out sale prices in stores, and understanding the nutritional information on food labels all involve percentages.
Common Mistakes in Percentage Calculations and How to Avoid Them
Several common pitfalls can lead to errors in percentage calculations:
1. Confusing the Whole and the Part: Ensure you correctly identify which value represents the whole (denominator) and which represents the part (numerator). Incorrectly identifying these values will lead to incorrect results.
2. Incorrect Order of Operations: When dealing with multiple percentage calculations, remember to follow the order of operations (PEMDAS/BODMAS). This helps maintain the accuracy of calculations involving parentheses, exponents, multiplication and division, addition, and subtraction.
3. Rounding Errors: Rounding numbers prematurely during intermediate steps can lead to significant errors in the final result. It's best to wait until the final step to round your answer to the desired level of precision.
4. Misunderstanding Percentage Increase and Decrease: Percentage increases and decreases are often confused. A 10% increase followed by a 10% decrease does not result in the original value; it results in a slightly lower value. Understanding the mathematical difference is critical.
Advanced Percentage Concepts
Moving beyond basic calculations, we can explore more advanced concepts:
1. Percentage Change: This measures the relative change between two values. The formula is: [(New Value - Old Value) / Old Value] × 100. A positive result indicates an increase, while a negative result indicates a decrease.
2. Compound Percentage Change: This refers to situations where the percentage change is applied repeatedly over time, such as compound interest.
3. Percentage Points: This is a crucial concept to understand. A percentage point represents an absolute change in percentage values. For example, an increase from 10% to 15% is a 5 percentage point increase, not a 50% increase.
4. Weighted Averages: These are averages where some values contribute more significantly than others based on their weights or proportions, often expressed as percentages.
Solving Real-World Problems Using Percentages
Let's apply these concepts to a few real-world examples:
Example 1: Sales Discount: A shirt is originally priced at $50, and a 20% discount is offered. What is the final price?
- Discount Amount: 20% of $50 = (20/100) * $50 = $10
- Final Price: $50 - $10 = $40
Example 2: Exam Scores: A student scores 45 out of 60 on an exam. What is their percentage score?
- Fraction: 45/60
- Decimal: 45 ÷ 60 = 0.75
- Percentage: 0.75 × 100 = 75%
Example 3: Percentage Increase: The population of a town increased from 1000 to 1200. What is the percentage increase?
- Percentage Change: [(1200 - 1000) / 1000] × 100 = 20%
Conclusion: Mastering Percentages for Success
Understanding percentages is a vital skill in various aspects of life, from personal finance to professional endeavors. While the basic calculation of "5 out of 8" is simple, grasping the underlying principles and mastering advanced concepts opens up opportunities for deeper analysis and problem-solving. By avoiding common mistakes and practicing regularly, you can confidently apply percentage calculations in any situation that requires this critical skill. The ability to interpret and work with percentages empowers you to make informed decisions and succeed in a data-driven world.
Latest Posts
Latest Posts
-
What Do You Call A Palace Window Answer Key
Jul 05, 2025
-
How Many Quarts In A 5 Gallon Bucket
Jul 05, 2025
-
How Far Is The Closest Ocean Beach To Me
Jul 05, 2025
-
How Long Is A China Man Joke
Jul 05, 2025
-
What Episode Does Ichigo Get His Powers Back
Jul 05, 2025
Related Post
Thank you for visiting our website which covers about Percentage Of 5 Out Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.