Power Series Ln 1 X 1 X
Kalali
May 30, 2025 · 3 min read
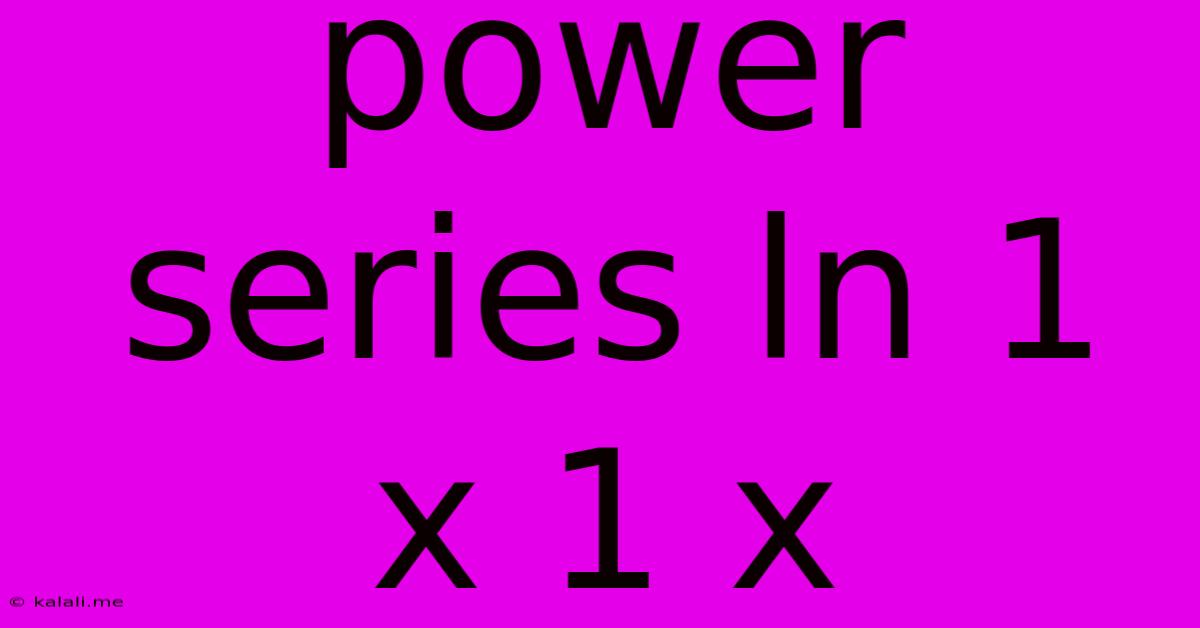
Table of Contents
Understanding the Power Series of ln(1 + x) and its Applications
The natural logarithm, often denoted as ln(x) or logₑ(x), is a fundamental function in mathematics with wide-ranging applications in calculus, physics, engineering, and computer science. Understanding its power series representation is crucial for approximating its value, solving differential equations, and performing other mathematical operations. This article delves into the power series expansion of ln(1 + x) and explores its practical uses. We'll cover its derivation, radius of convergence, and applications in various fields.
The power series for ln(1 + x) is given by:
ln(1 + x) = Σ (from n=1 to ∞) (-1)^(n+1) * (xⁿ/n) = x - x²/2 + x³/3 - x⁴/4 + ...
This series converges for -1 < x ≤ 1. Let's explore this further:
Derivation of the Power Series
The power series is derived using the geometric series and integration. Recall the geometric series:
1/(1 + x) = Σ (from n=0 to ∞) (-x)ⁿ = 1 - x + x² - x³ + ... (for |x| < 1)
Integrating both sides with respect to x, we get:
∫ 1/(1 + x) dx = ∫ Σ (from n=0 to ∞) (-x)ⁿ dx
ln|1 + x| + C = Σ (from n=0 to ∞) (-1)ⁿ * (xⁿ⁺¹/(n + 1))
Setting x = 0, we find that C = 0. Reindexing the summation, we arrive at the power series for ln(1 + x):
ln(1 + x) = Σ (from n=1 to ∞) (-1)^(n+1) * (xⁿ/n)
Radius of Convergence
The radius of convergence for this power series is 1. This means the series converges for -1 < x ≤ 1. At x = -1, the series becomes the alternating harmonic series, which converges by the alternating series test. At x = 1, it becomes the alternating harmonic series, which also converges. Outside this interval, the series diverges.
Applications of the Power Series
The power series representation of ln(1 + x) has numerous applications:
-
Approximation of ln(1 + x): For values of x within the interval of convergence, the power series provides an accurate approximation of ln(1 + x). The more terms included in the summation, the more precise the approximation becomes. This is particularly useful when calculating natural logarithms without a calculator, especially for values close to 0.
-
Solving Differential Equations: The power series can be used to find series solutions to certain types of differential equations. By substituting the power series into the differential equation, one can solve for the coefficients of the series.
-
Numerical Integration: The power series can simplify complex integrals that are difficult to solve analytically. Replacing the function with its power series representation can sometimes lead to easier integration.
-
Taylor and Maclaurin Series: The power series is a specific example of a Taylor series centered at x = 0 (a Maclaurin series). Understanding this relationship helps in developing other Taylor and Maclaurin series expansions.
-
Analysis of Functions Near a Point: The power series provides local information about the function ln(1 + x) around x = 0. This can be valuable for analyzing the function's behavior near that point.
Conclusion
The power series expansion of ln(1 + x) is a powerful tool with significant applications across various mathematical disciplines and scientific fields. Its derivation from the geometric series, its radius of convergence, and its practical uses in approximation, differential equations, and numerical integration make it an essential concept for anyone studying calculus and related fields. Understanding this series deepens one's understanding of function approximation and series manipulation, building a strong foundation for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
Toilet Bowl Water Level Slowly Drops
Jun 01, 2025
-
Brown Spots Inside Bell Pepper Safe To Eat
Jun 01, 2025
-
Logos Start On A New Line
Jun 01, 2025
-
How To Get A Supplie Id
Jun 01, 2025
-
How Do You Say For In German
Jun 01, 2025
Related Post
Thank you for visiting our website which covers about Power Series Ln 1 X 1 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.