Power Series Of 1 1 X
Kalali
May 24, 2025 · 3 min read
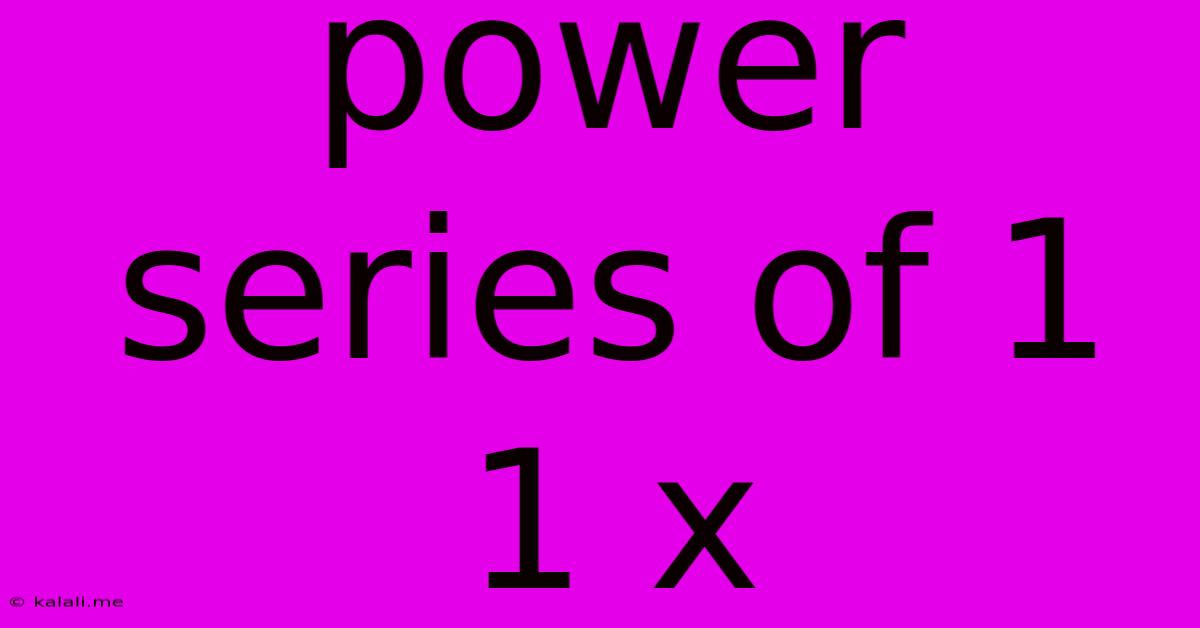
Table of Contents
Power Series Representation of 1/(1+x)
This article explores the power series representation of the function f(x) = 1/(1+x), a crucial concept in calculus and its applications. We'll derive the series, discuss its radius and interval of convergence, and touch upon its uses in various mathematical fields. Understanding this power series is fundamental for tackling more complex problems in analysis and other areas.
The power series representation of 1/(1+x) is a geometric series, making its derivation relatively straightforward. Remember that a geometric series converges to a/(1-r) when |r| < 1, where 'a' is the first term and 'r' is the common ratio.
Deriving the Power Series
Let's rewrite 1/(1+x) as 1/(1 - (-x)). This puts it in the form of a geometric series where a = 1 and r = -x. Applying the formula for the sum of an infinite geometric series, we get:
1/(1+x) = 1 + (-x) + (-x)² + (-x)³ + ... = Σ (-x)^n, where n ranges from 0 to infinity.
This simplifies to:
1/(1+x) = Σ (-1)^n * x^n, for |x| < 1
This is the power series representation of 1/(1+x). It's a simple yet powerful tool with wide-ranging applications.
Radius and Interval of Convergence
The series converges when the absolute value of the common ratio, |-x|, is less than 1. This gives us:
|-x| < 1 => |x| < 1
Therefore, the radius of convergence is 1.
To determine the interval of convergence, we need to check the endpoints, x = -1 and x = 1.
- At x = -1: The series becomes Σ (-1)^n * (-1)^n = Σ 1, which diverges.
- At x = 1: The series becomes Σ (-1)^n, which is the alternating harmonic series, and it converges by the Alternating Series Test.
Thus, the interval of convergence is (-1, 1].
Applications of the Power Series
The power series representation of 1/(1+x) has significant applications in various areas of mathematics:
- Calculus: It's used in evaluating integrals that are difficult or impossible to solve using elementary techniques. By substituting the power series, you can often integrate term by term to obtain an approximate solution or an exact solution expressed as an infinite series.
- Differential Equations: Power series solutions are frequently employed to solve differential equations, particularly those that don't have simple closed-form solutions. This power series can be a component within larger series solutions.
- Approximations: The series provides a way to approximate the value of 1/(1+x) for values of x within the interval of convergence. The more terms you include, the more accurate the approximation becomes. This is especially useful in numerical analysis and computer science.
- Complex Analysis: This power series extends to the complex plane, offering insights into the behavior of complex functions and providing tools for complex integration.
Conclusion
The power series representation of 1/(1+x) is a fundamental concept with far-reaching implications. Understanding its derivation, convergence properties, and applications is crucial for anyone studying calculus, analysis, or related fields. This seemingly simple series serves as a building block for more advanced mathematical techniques and problem-solving strategies. Its versatility makes it an invaluable tool in both theoretical and practical applications.
Latest Posts
Latest Posts
-
How To Trim Nails Without Clippers
May 24, 2025
-
Garage Door Will Go Up But Not Down
May 24, 2025
-
Pay To The Order Of Cash
May 24, 2025
-
In The Beginning At The Beginning
May 24, 2025
-
How To Pull Up Carpet Without Damaging It
May 24, 2025
Related Post
Thank you for visiting our website which covers about Power Series Of 1 1 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.