Roots Of X 2 X 1
Kalali
Jun 01, 2025 · 3 min read
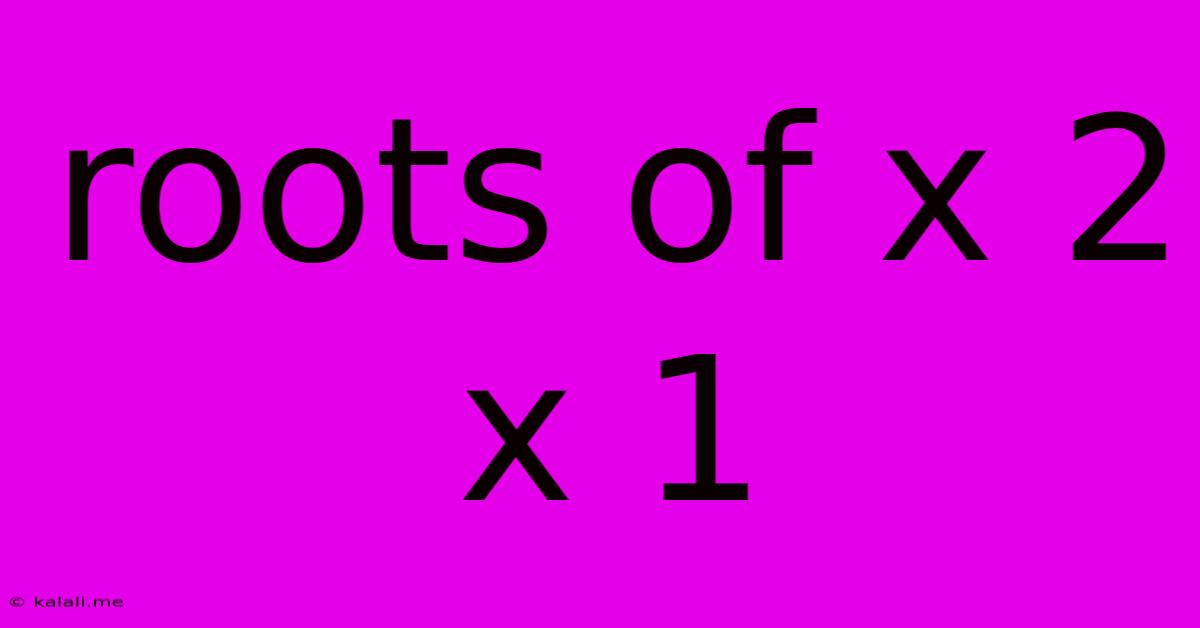
Table of Contents
Solving the Quadratic Equation: x² + 2x + 1 = 0
This article explores the solution to the quadratic equation x² + 2x + 1 = 0, explaining the different methods available and providing a comprehensive understanding of the underlying mathematical principles. We will delve into factoring, the quadratic formula, and completing the square, offering a versatile approach to solving this specific equation and similar quadratic problems. This will help you understand not just the answer, but the why behind it.
Understanding Quadratic Equations
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (x in this case) is 2. They generally take the form ax² + bx + c = 0, where a, b, and c are constants and a ≠ 0. Our specific equation, x² + 2x + 1 = 0, has a = 1, b = 2, and c = 1. Understanding these coefficients is crucial for choosing the most efficient solution method.
Method 1: Factoring
Factoring is often the quickest method for solving quadratic equations, especially when the equation can be easily factored. In this case, x² + 2x + 1 is a perfect square trinomial. This means it can be factored into the square of a binomial:
(x + 1)(x + 1) = 0 or (x + 1)² = 0
This simplifies the solution considerably. To find the roots, we set each factor equal to zero:
x + 1 = 0
Solving for x, we get:
x = -1
Therefore, the equation x² + 2x + 1 = 0 has only one real root, x = -1. This is because the quadratic represents a parabola that touches the x-axis at only one point.
Method 2: The Quadratic Formula
The quadratic formula is a more general method that works for all quadratic equations, even those that are difficult or impossible to factor. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
Plugging in the values from our equation (a = 1, b = 2, c = 1), we get:
x = [-2 ± √(2² - 4 * 1 * 1)] / (2 * 1) x = [-2 ± √(4 - 4)] / 2 x = [-2 ± √0] / 2 x = -2 / 2 x = -1
Again, we find that the only root is x = -1.
Method 3: Completing the Square
Completing the square is another powerful technique for solving quadratic equations. It involves manipulating the equation to create a perfect square trinomial, which can then be easily factored.
Starting with x² + 2x + 1 = 0:
-
Move the constant term to the right side: x² + 2x = -1
-
Take half of the coefficient of x (which is 2), square it (2/2 = 1, 1² = 1), and add it to both sides: x² + 2x + 1 = -1 + 1
-
Factor the left side as a perfect square: (x + 1)² = 0
-
Solve for x: x + 1 = 0 x = -1
Conclusion
All three methods demonstrate that the quadratic equation x² + 2x + 1 = 0 has a single real root at x = -1. Understanding these different approaches provides you with a versatile toolkit for solving a wide range of quadratic equations. Choosing the most appropriate method depends on the specific equation and your personal preference. This equation, being a perfect square trinomial, lends itself particularly well to factoring, but the quadratic formula and completing the square offer robust alternatives for more complex scenarios.
Latest Posts
Latest Posts
-
Farming A Man Of Your Talents
Jun 02, 2025
-
Business In The Front Party In Back
Jun 02, 2025
-
All I Know Is My Electric Drill Floated
Jun 02, 2025
-
What To Do After Killing First Mechanical Boss
Jun 02, 2025
-
Do Pans Need A Higher Or Lower Specific Heat
Jun 02, 2025
Related Post
Thank you for visiting our website which covers about Roots Of X 2 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.