Round The Value 44.981 G To Three Significant Figures.
Kalali
Jul 28, 2025 · 7 min read
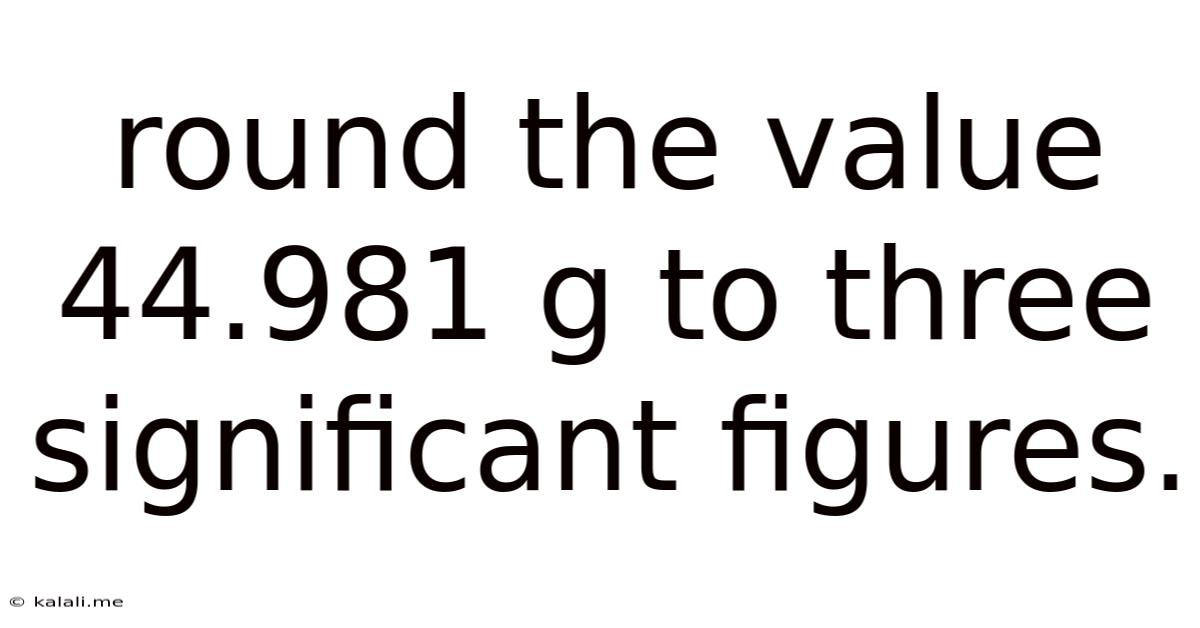
Table of Contents
Rounding to Significant Figures: A Deep Dive into the 44.981 g Example
Rounding numbers is a fundamental skill in mathematics and science, crucial for presenting data clearly and concisely. This process is particularly important when dealing with measurements, where the precision of the instrument used dictates the number of significant figures. This article will explore the concept of rounding, focusing specifically on rounding the value 44.981 g to three significant figures. We'll cover the rules of rounding, the importance of significant figures, and delve into practical applications and potential pitfalls. Understanding this seemingly simple concept lays the groundwork for more advanced scientific and mathematical endeavors.
Meta Description: Learn how to round numbers to significant figures, using the example of 44.981 g rounded to three significant figures. This comprehensive guide covers the rules, importance, and practical applications of rounding in science and mathematics.
Understanding Significant Figures
Before we tackle the rounding of 44.981 g, let's establish a clear understanding of significant figures. Significant figures (sig figs) are the digits in a number that carry meaning contributing to its precision. They represent the level of accuracy of a measurement. Not all digits in a number are significant; some are simply placeholders.
Here's a breakdown of rules for determining significant figures:
- All non-zero digits are significant. For example, in the number 123, all three digits are significant.
- Zeros between non-zero digits are significant. In the number 102, the zero is significant.
- Leading zeros (zeros to the left of the first non-zero digit) are not significant. In 0.0012, only 1 and 2 are significant.
- Trailing zeros (zeros to the right of the last non-zero digit) in a number containing a decimal point are significant. In 1.200, all four digits are significant.
- Trailing zeros in a number without a decimal point are ambiguous and should be avoided by using scientific notation. For example, 1200 could have two, three, or four significant figures. Scientific notation (1.2 x 10³ or 1.20 x 10³ or 1.200 x 10³) removes the ambiguity.
Rounding Rules
The process of rounding involves adjusting a number to a certain level of precision. When rounding to a specific number of significant figures, we follow these steps:
- Identify the digit to be rounded. This is the digit one place to the right of the last significant figure you wish to keep.
- Look at the digit immediately to the right of the digit to be rounded.
- If this digit is 5 or greater, round up (add 1 to the digit being rounded).
- If this digit is less than 5, keep the digit being rounded as it is.
- Drop all digits to the right of the rounded digit.
Rounding 44.981 g to Three Significant Figures
Now, let's apply these rules to our example: 44.981 g. We need to round this value to three significant figures.
- Identify the digit to be rounded: The third significant figure is 9. The digit to be rounded is the one immediately to the right, which is 8.
- Look at the digit to the right of the digit to be rounded: This is 1.
- Since 1 is less than 5, we keep the digit 9 as it is.
- Drop all digits to the right of 9: We remove the 8 and the 1.
Therefore, 44.981 g rounded to three significant figures is 45.0 g. Notice that we retain the trailing zero to indicate the precision to one decimal place, even though it's a trailing zero. This is crucial for maintaining the correct number of significant figures. Leaving it as 45 g would imply only two significant figures.
Importance of Significant Figures in Scientific Measurements
The correct use of significant figures is paramount in scientific and engineering applications for several reasons:
- Accurate Representation of Data: Significant figures reflect the precision of the measuring instrument used. Using more significant figures than are justified by the measurement implies a greater accuracy than actually exists, while using fewer significant figures hides potentially relevant information.
- Propagation of Errors: Rounding errors can accumulate during calculations. Using an appropriate number of significant figures helps minimize the impact of these errors on the final result. This is especially crucial in complex calculations involving many steps.
- Clear Communication of Results: Consistent use of significant figures ensures that the results are communicated clearly and accurately. Readers can understand the level of uncertainty associated with the measurements and calculations.
- Avoiding Misinterpretations: Incorrect handling of significant figures can lead to misinterpretations and erroneous conclusions. This could have significant implications in fields like medicine, engineering, and environmental science, where even small errors can have far-reaching consequences.
Consider a scenario where you're measuring the mass of a chemical compound during an experiment. Your scale is precise to three decimal places, giving you a reading of 44.981 g. Reporting this value as 45 g may seem simpler, but it masks the precision of your measurement. It also makes it more difficult to perform calculations that require the original degree of accuracy.
Practical Applications and Examples
Rounding to significant figures is widely used across various disciplines:
- Chemistry: Determining the molar mass of a compound, calculating reaction yields, and analyzing experimental data.
- Physics: Analyzing experimental results, reporting measurements of physical quantities (like length, mass, time), and solving problems involving calculations with measured values.
- Engineering: Designing structures, calculating stresses and strains, and performing simulations.
- Finance: Rounding monetary values to two decimal places, calculating interest rates, and performing financial modeling.
- Data Analysis: Presenting data in charts and graphs, calculating averages and standard deviations, and presenting data summaries.
Advanced Rounding Scenarios and Considerations
While the basic rules of rounding are relatively straightforward, some scenarios require additional consideration:
- Rounding to a specific decimal place: The focus shifts from significant figures to the position of the decimal point. For example, rounding 44.981 g to one decimal place would result in 45.0 g.
- Rounding with multiple operations: When performing multiple calculations, it's recommended to retain a few extra significant figures during intermediate steps before performing the final rounding to avoid accumulation of rounding errors.
- Rounding and scientific notation: Combining rounding with scientific notation is crucial for expressing very large or very small numbers while maintaining the appropriate number of significant figures. For example, 6,500,000 rounded to two significant figures would be 6.5 x 10⁶.
Common Mistakes to Avoid
Several common mistakes can arise when rounding numbers to significant figures:
- Incorrect identification of significant figures: Misinterpreting the rules for identifying significant figures can lead to incorrect rounding. Careful attention to the rules is vital.
- Premature rounding: Rounding intermediate results in a multi-step calculation can lead to a significant loss of accuracy in the final answer. It's best practice to keep extra significant figures during calculations and only round the final result.
- Ignoring trailing zeros: Trailing zeros after the decimal point are significant and should be retained to indicate the precision of the measurement.
- Inconsistency in application: Applying the rounding rules inconsistently can lead to inaccurate and unreliable results. Maintaining consistency is crucial for accurate representation of data.
Conclusion
Rounding numbers to a specified number of significant figures is a fundamental skill in mathematics and science. Understanding the rules of rounding and the importance of significant figures is crucial for accurately representing data, minimizing errors in calculations, and clearly communicating results. While the process may seem simple at first glance, paying close attention to detail and avoiding common mistakes is essential for producing accurate and reliable results across various disciplines. The example of rounding 44.981 g to three significant figures (resulting in 45.0 g) perfectly illustrates the core principles and their importance in maintaining the integrity of scientific and numerical data. The meticulous application of these rules ensures clarity, precision, and the avoidance of misinterpretations in scientific and mathematical work.
Latest Posts
Latest Posts
-
How Many Cups Are In 4 L
Jul 29, 2025
-
Why Is It 1500m And Not 1600m
Jul 29, 2025
-
Take Me In To The Holy Of Holies
Jul 29, 2025
-
Is It Illegal To Dumpster Dive In Pennsylvania
Jul 29, 2025
-
How Many Liters In A Can Of Soda
Jul 29, 2025
Related Post
Thank you for visiting our website which covers about Round The Value 44.981 G To Three Significant Figures. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.