Scatter Plots And Line Of Best Fit
Kalali
Apr 02, 2025 · 6 min read
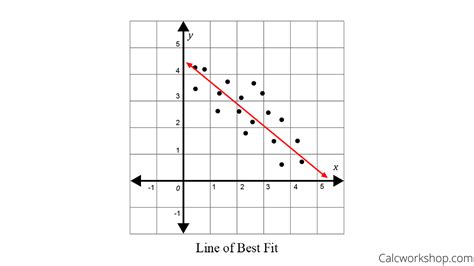
Table of Contents
Scatter Plots and the Line of Best Fit: A Comprehensive Guide
Scatter plots are a fundamental tool in statistics used to visualize the relationship between two variables. They provide a powerful way to identify trends, correlations, and potential outliers within a dataset. Understanding how to interpret scatter plots, and particularly how to calculate and interpret the line of best fit (also known as the regression line), is crucial for anyone working with data analysis. This comprehensive guide will explore scatter plots and lines of best fit in detail, covering their creation, interpretation, and applications.
What is a Scatter Plot?
A scatter plot is a type of graph that displays data as a collection of points, each having the value of one variable determining the position on the horizontal axis and the value of the other variable determining the position on the vertical axis. The resulting visual representation shows the relationship—or lack thereof—between the two variables. The variables are often denoted as the independent variable (x-axis) and the dependent variable (y-axis). The independent variable is the one that is manipulated or changed, while the dependent variable is the one that is measured or observed.
Key Features of a Scatter Plot:
- Independent Variable (x-axis): This variable is typically the one that is thought to influence the dependent variable.
- Dependent Variable (y-axis): This variable is the one that is being measured or observed.
- Data Points: Each point on the scatter plot represents a single observation or data point, with its coordinates corresponding to the values of the two variables.
- Clusters and Patterns: The arrangement of points can reveal patterns, clusters, or trends within the data.
- Outliers: Points that deviate significantly from the overall pattern are considered outliers. These can be influential in analysis and warrant further investigation.
Interpreting Scatter Plots: Identifying Correlations
The visual arrangement of points in a scatter plot reveals the nature of the relationship between the two variables. We can categorize the correlation as follows:
- Positive Correlation: As the independent variable increases, the dependent variable also increases. The points tend to cluster around a line sloping upwards from left to right.
- Negative Correlation: As the independent variable increases, the dependent variable decreases. The points tend to cluster around a line sloping downwards from left to right.
- No Correlation: There is no discernible relationship between the variables. The points appear randomly scattered with no clear pattern.
- Non-Linear Correlation: The relationship between the variables is not linear; it might follow a curve or other non-straight-line pattern.
Strength of Correlation:
The strength of the correlation is indicated by how closely the points cluster around a potential line. A strong correlation shows points tightly clustered, while a weak correlation shows points more spread out. This strength is often quantified using a statistical measure called the correlation coefficient (r), which ranges from -1 to +1.
- r = +1: Perfect positive correlation
- r = -1: Perfect negative correlation
- r = 0: No correlation
- Values between -1 and +1: Indicate varying degrees of correlation strength. Values closer to +1 or -1 signify stronger correlations.
The Line of Best Fit (Regression Line)
The line of best fit is a straight line that best represents the trend in a scatter plot. It aims to minimize the overall distance between the line and all the data points. This line provides a simplified representation of the relationship between the variables and allows for predictions. The most common method for determining the line of best fit is the method of least squares.
Method of Least Squares:
The method of least squares aims to find the line that minimizes the sum of the squared vertical distances between each data point and the line. This method provides a mathematically optimal fit. The equation of the line of best fit is typically represented as:
y = mx + c
Where:
- y: The dependent variable
- x: The independent variable
- m: The slope of the line (representing the rate of change of y with respect to x)
- c: The y-intercept (the value of y when x = 0)
Calculating the Line of Best Fit:
Calculating the slope (m) and y-intercept (c) involves using the following formulas:
m = Σ[(xi - x̄)(yi - ȳ)] / Σ[(xi - x̄)²]
c = ȳ - m x̄
Where:
- xi and yi: Individual data points
- x̄ and ȳ: The means (averages) of the x and y values respectively
- Σ: Represents the sum of the values
These calculations can be performed manually or more easily using statistical software or spreadsheets.
Applications of Scatter Plots and Lines of Best Fit
Scatter plots and lines of best fit have numerous applications across various fields, including:
- Science: Analyzing relationships between variables in experiments, like the effect of fertilizer on plant growth.
- Economics: Modeling economic relationships, such as the correlation between inflation and unemployment.
- Business: Forecasting sales based on advertising spending, analyzing customer behavior.
- Engineering: Evaluating the performance of materials under different conditions.
- Medicine: Studying the relationship between risk factors and disease incidence.
- Environmental Science: Analyzing the relationship between pollution levels and environmental health.
Making Predictions:
Once the line of best fit is established, it can be used to make predictions about the dependent variable based on the independent variable. However, it's crucial to remember that predictions are most reliable within the range of the data used to create the line. Extrapolating beyond this range can lead to unreliable results.
Limitations of Scatter Plots and Lines of Best Fit
While scatter plots and lines of best fit are powerful tools, it's essential to be aware of their limitations:
- Correlation does not equal causation: A strong correlation between two variables doesn't necessarily mean one causes the other. There might be other underlying factors or confounding variables at play.
- Outliers: Outliers can significantly influence the position of the line of best fit, potentially skewing the results. Careful consideration of outliers is needed.
- Linearity Assumption: The method assumes a linear relationship between the variables. If the relationship is non-linear, the line of best fit might not be an accurate representation.
- Data Quality: The accuracy of the analysis depends on the quality of the data used. Errors in data collection can lead to misleading results.
Advanced Concepts
For a more in-depth understanding, consider exploring these advanced concepts:
- Correlation Coefficient (r): This quantifies the strength and direction of the linear relationship between two variables.
- Coefficient of Determination (r²): This indicates the proportion of variance in the dependent variable that is explained by the independent variable.
- Residual Analysis: Examining the residuals (the differences between the observed values and the values predicted by the line of best fit) can help assess the validity of the model.
- Multiple Linear Regression: This extends the concept to analyze the relationship between a dependent variable and multiple independent variables.
Conclusion
Scatter plots and lines of best fit are essential tools for visualizing and analyzing the relationship between two variables. Understanding how to create, interpret, and apply these techniques is crucial for anyone working with data. Remember to consider the limitations and explore advanced concepts to enhance the accuracy and reliability of your analysis. By carefully interpreting scatter plots and using the line of best fit appropriately, you can gain valuable insights from your data and make informed decisions. Always remember that responsible data analysis requires critical thinking and awareness of potential biases and limitations.
Latest Posts
Latest Posts
-
What Is 20 Percent Of 800 000
Jul 12, 2025
-
Words That Start With Y In Science
Jul 12, 2025
-
Prevent An Expressway Emergency By Merging Without
Jul 12, 2025
-
How Many Grams Of Sugar In A Pound
Jul 12, 2025
-
7am To 11am Is How Many Hours
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about Scatter Plots And Line Of Best Fit . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.