Seven Less Than A Number Is 15
Kalali
Aug 24, 2025 · 5 min read
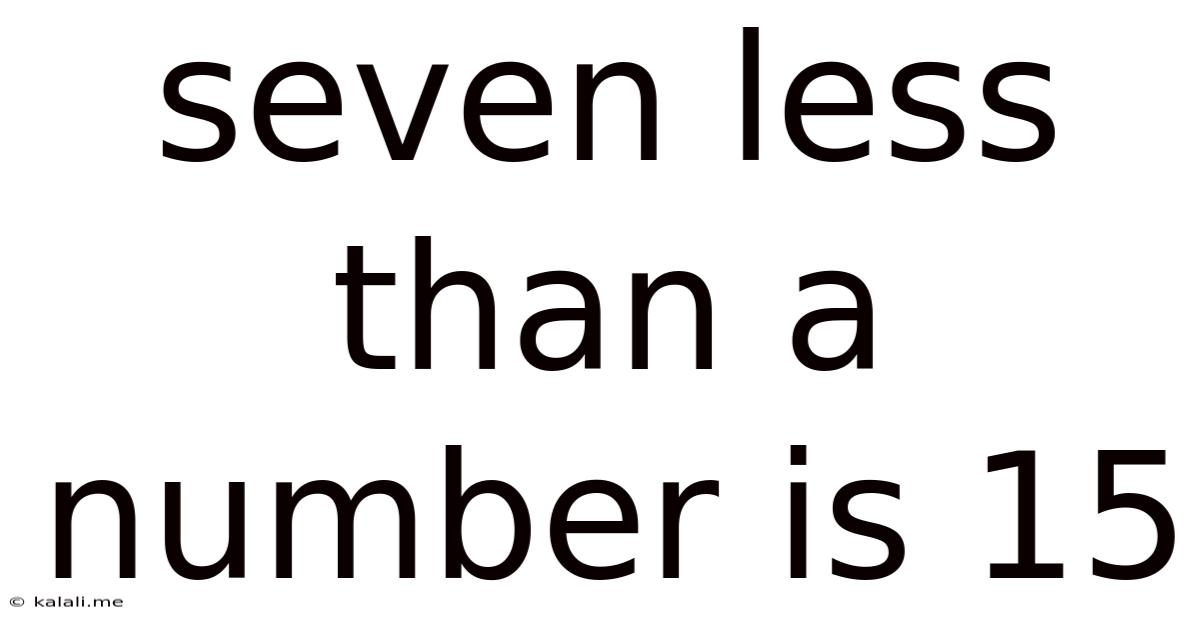
Table of Contents
Seven Less Than a Number is 15: Unveiling the Power of Algebraic Equations
This seemingly simple statement, "Seven less than a number is 15," holds the key to understanding fundamental algebraic concepts. This article will not only solve the equation but will delve deep into the underlying principles, providing a comprehensive guide for beginners and a refresher for those needing a boost in their algebra skills. We'll explore various approaches to solving this problem, examine related concepts, and discuss the broader applications of algebraic equations in real-world scenarios. By the end, you'll not only know the answer but also understand the why behind the solution.
Meta Description: Learn how to solve the algebraic equation "Seven less than a number is 15." This comprehensive guide covers various methods, explains related concepts, and explores real-world applications. Master fundamental algebra skills!
Understanding the Problem: Deconstructing the Statement
Before diving into the solution, let's break down the statement "Seven less than a number is 15" into its component parts. This seemingly simple sentence hides a powerful mathematical relationship.
- "A number": This represents an unknown quantity, which we'll typically denote with a variable, usually 'x' or 'n'.
- "Seven less than": This indicates subtraction. We're taking seven away from our unknown number.
- "is 15": This signifies equality. The result of subtracting seven from the number is equal to fifteen.
Therefore, we can translate the sentence into a mathematical equation: x - 7 = 15
Method 1: Solving the Equation Using Inverse Operations
The most straightforward method to solve this equation involves using inverse operations. Inverse operations are operations that "undo" each other. Addition and subtraction are inverse operations, as are multiplication and division.
-
Isolate the variable: Our goal is to isolate 'x' on one side of the equation. To do this, we need to undo the subtraction of 7. The inverse operation of subtraction is addition.
-
Add 7 to both sides: To maintain the balance of the equation, whatever we do to one side, we must do to the other. Adding 7 to both sides gives us:
x - 7 + 7 = 15 + 7 -
Simplify: This simplifies to:
x = 22
Therefore, the number is 22. Let's check our work: 22 - 7 = 15. Our solution is correct!
Method 2: Using a Balance Scale Analogy
Visualizing the equation using a balance scale can be incredibly helpful, especially for beginners. Imagine a balance scale with x - 7 on one side and 15 on the other. To keep the scale balanced, we must perform the same operation on both sides.
-
Adding weight: To isolate 'x', we add 7 units of weight to both sides of the scale.
-
Maintaining balance: This cancels out the -7 on the left side, leaving only 'x'. On the right side, we now have 15 + 7 = 22.
-
The solution: The scale balances when x = 22.
Method 3: Transposing Terms
This method is a shorthand version of the inverse operation method. It involves moving terms from one side of the equation to the other, changing their sign in the process.
-
Transpose -7: The term '-7' is transposed to the right-hand side, becoming '+7'.
-
Simplified equation: This leaves us with:
x = 15 + 7 -
Solution: Therefore,
x = 22.
Expanding the Understanding: Related Concepts
Solving "Seven less than a number is 15" introduces us to several crucial algebraic concepts:
-
Variables: The use of 'x' (or any letter) to represent an unknown quantity is fundamental to algebra.
-
Equations: An equation shows the equality between two expressions. Solving an equation means finding the value(s) of the variable(s) that make the equation true.
-
Inverse Operations: Understanding inverse operations is key to manipulating equations and isolating variables.
-
Balancing Equations: The principle of maintaining balance by performing the same operation on both sides of the equation is critical for accurate solutions.
-
Solving for Unknowns: This problem exemplifies the core goal of algebra: finding unknown values using known relationships.
Real-World Applications of Algebraic Equations
Algebraic equations, seemingly abstract, are powerful tools used extensively in various real-world scenarios. Here are a few examples:
-
Finance: Calculating interest, determining loan repayments, and analyzing investment returns all involve solving algebraic equations.
-
Physics: Newton's laws of motion, equations of energy, and many other physical phenomena are described using algebraic equations.
-
Engineering: Designing structures, calculating forces, and analyzing systems often require solving complex algebraic equations.
-
Computer Science: Programming algorithms, developing software, and managing data structures frequently use algebraic concepts.
-
Everyday Problem Solving: Many everyday problems, from calculating discounts to figuring out how much paint you need, can be solved using simple algebraic equations.
Extending the Challenge: More Complex Problems
While "Seven less than a number is 15" is a simple equation, it lays the groundwork for solving much more complex algebraic problems. Consider these examples:
-
Two-step equations:
2x + 5 = 11(requires multiple steps to isolate x) -
Equations with fractions:
(x/2) - 3 = 7(requires dealing with fractions) -
Equations with decimals:
0.5x + 2.5 = 5(requires understanding decimal operations) -
Inequalities:
x - 7 > 15(deals with greater than or less than relationships) -
Systems of equations: A set of two or more equations with two or more variables, requiring simultaneous solution.
Conclusion: Mastering the Fundamentals
Solving "Seven less than a number is 15" is more than just finding the answer; it's about grasping the fundamental principles of algebra. This seemingly simple problem opens the door to a world of mathematical possibilities, empowering you to solve complex problems and apply algebraic concepts to various real-world situations. By mastering these fundamental techniques, you build a solid foundation for future mathematical explorations and applications. Remember to practice regularly, explore different problem-solving methods, and don't be afraid to seek help when needed. The journey of mastering algebra is rewarding, and this simple equation is just the first step on that journey.
Latest Posts
Latest Posts
-
How Fast Does A Ktm 65 Sx Go
Aug 24, 2025
-
Which Number Produces An Irrational Number When Multiplied By 1 3
Aug 24, 2025
-
How Much Does An Empty Aluminum Can Weigh
Aug 24, 2025
-
How Many Inches Is 2 3 Of A Yard
Aug 24, 2025
-
In The Actual Economy Goods And Services Are Purchased By
Aug 24, 2025
Related Post
Thank you for visiting our website which covers about Seven Less Than A Number Is 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.