Seven Less Than Twice A Number Is 5
Kalali
Aug 25, 2025 · 5 min read
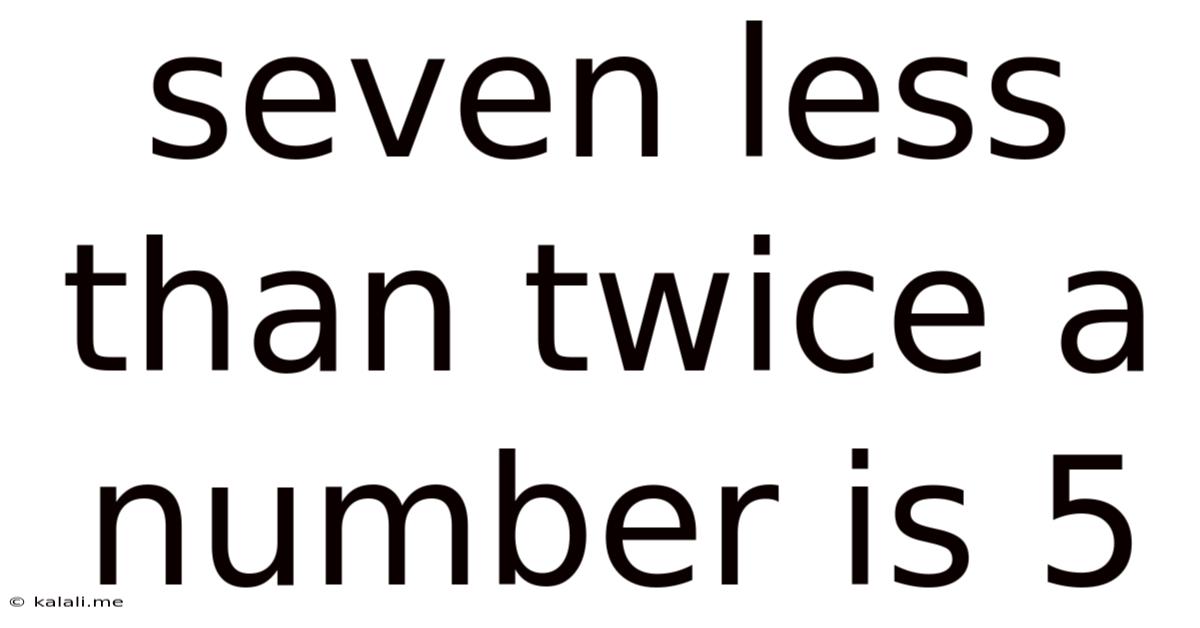
Table of Contents
Seven Less Than Twice a Number Is 5: Unraveling the Equation and its Applications
This seemingly simple statement, "Seven less than twice a number is 5," hides a powerful concept within the realm of algebra. It introduces us to the world of translating words into mathematical equations and solving for the unknown. This article will not only solve this specific equation but also explore the broader implications of such problems, examining their applications in various fields and delving into the underlying mathematical principles. Understanding this type of problem is crucial for anyone studying algebra, and its applications extend far beyond the classroom.
Understanding the Problem: From Words to Equations
The phrase "Seven less than twice a number is 5" might seem daunting at first, but breaking it down step-by-step reveals its inherent simplicity. Let's dissect each part:
- "A number": This represents our unknown, which we can denote with a variable, typically 'x'.
- "Twice a number": This translates to 2x (two times the number).
- "Seven less than twice a number": This means we subtract 7 from 2x, resulting in the expression 2x - 7.
- "Is 5": This indicates equality, meaning the expression 2x - 7 equals 5.
Therefore, the complete mathematical equation becomes: 2x - 7 = 5
Solving the Equation: Finding the Value of 'x'
Now that we have the equation, solving for 'x' involves a series of algebraic manipulations. Our goal is to isolate 'x' on one side of the equation. Here's how we do it:
-
Add 7 to both sides: This eliminates the -7 from the left side, giving us: 2x - 7 + 7 = 5 + 7 2x = 12
-
Divide both sides by 2: This isolates 'x', revealing its value: 2x / 2 = 12 / 2 x = 6
Therefore, the number we're looking for is 6. We can verify this by substituting 6 back into the original equation: 2(6) - 7 = 12 - 7 = 5. The equation holds true.
Beyond the Basics: Expanding the Concept
While seemingly straightforward, this simple equation embodies fundamental algebraic principles that underpin more complex mathematical concepts and real-world applications. Let's explore some of these:
1. Applications in Real-World Scenarios
Word problems like this one aren't just abstract exercises; they model numerous real-life situations. Consider these examples:
- Profit Calculation: A business owner might use a similar equation to calculate the number of units they need to sell to reach a specific profit target, considering production costs and profit margins.
- Financial Planning: Determining the amount of money needed to save for a down payment on a house or a large purchase might involve setting up and solving an equation similar to this.
- Physics and Engineering: Many physics and engineering problems involve setting up equations to model relationships between variables, and solving for unknown quantities.
- Chemistry and Biology: Stoichiometry in chemistry, for instance, frequently uses equations to relate the quantities of reactants and products in chemical reactions.
2. Understanding Variables and Equations
The use of variables (like 'x') to represent unknown quantities is a cornerstone of algebra. It allows us to create generalizable models and solve for unknown values within a defined system. The concept of an equation, a statement of equality between two expressions, is fundamental to mathematical modeling.
3. Developing Problem-Solving Skills
Solving word problems, such as "Seven less than twice a number is 5," enhances critical thinking and problem-solving skills. It teaches us to break down complex information into smaller, manageable steps, translate words into mathematical language, and employ systematic methods to find solutions.
4. Linear Equations and Their Graphs
The equation 2x - 7 = 5 is a linear equation. Linear equations are characterized by their straight-line graphs when plotted on a coordinate plane. Understanding the graphical representation of linear equations provides further insight into the relationship between the variables. The solution to the equation (x=6) represents the x-intercept of the line representing the equation y = 2x - 7.
5. Inequalities and Advanced Concepts
While this specific problem deals with an equation, the principles involved can be extended to inequalities. For example, we could modify the problem to say "Seven less than twice a number is greater than or equal to 5," which would lead to an inequality (2x - 7 ≥ 5) requiring different solution techniques. This opens the door to more complex mathematical concepts, including systems of equations and inequalities.
6. Importance of Verification
After solving an equation, it's crucial to verify the solution by substituting the value back into the original equation. This ensures the accuracy of the obtained solution and reinforces the understanding of the equation's meaning. In more complex problems, verification becomes even more critical.
Expanding the Problem: Variations and Extensions
Let's explore some variations and extensions of the initial problem to further solidify the underlying concepts:
- "Five more than twice a number is 17": This variation would translate to the equation 2x + 5 = 17, requiring similar algebraic manipulation to solve.
- "Three less than half a number is 8": This changes the coefficients and constant, leading to the equation (x/2) - 3 = 8.
- Systems of Equations: Imagine we have a second equation involving the same unknown variable 'x'. Solving a system of equations would require the use of techniques like substitution or elimination. For instance, we might have the system: 2x - 7 = 5 x + y = 10 Solving this system would yield the values of both 'x' and 'y'.
Conclusion: A Foundation for Further Mathematical Exploration
The seemingly simple statement, "Seven less than twice a number is 5," provides a robust introduction to fundamental algebraic concepts. Solving this equation not only provides a numerical answer but lays the groundwork for a deeper understanding of variables, equations, problem-solving strategies, and their vast applications across various disciplines. By mastering these foundational elements, individuals pave the way for more advanced mathematical explorations and successful problem-solving in numerous real-world scenarios. The ability to translate word problems into mathematical equations and solve for unknowns is an invaluable skill applicable far beyond the confines of a mathematics classroom.
Latest Posts
Latest Posts
-
Pounds Per Acre To Kg Per Hectare
Aug 26, 2025
-
3 Quarts Of Water Equals How Many Cups
Aug 26, 2025
-
What Is A Group Of Wasps Called
Aug 26, 2025
-
What Is A Hundredth Of A Second
Aug 26, 2025
-
How Much Water Is In Dr Pepper
Aug 26, 2025
Related Post
Thank you for visiting our website which covers about Seven Less Than Twice A Number Is 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.