Sin 2x 1 Cos 2x 2
Kalali
Jun 10, 2025 · 2 min read
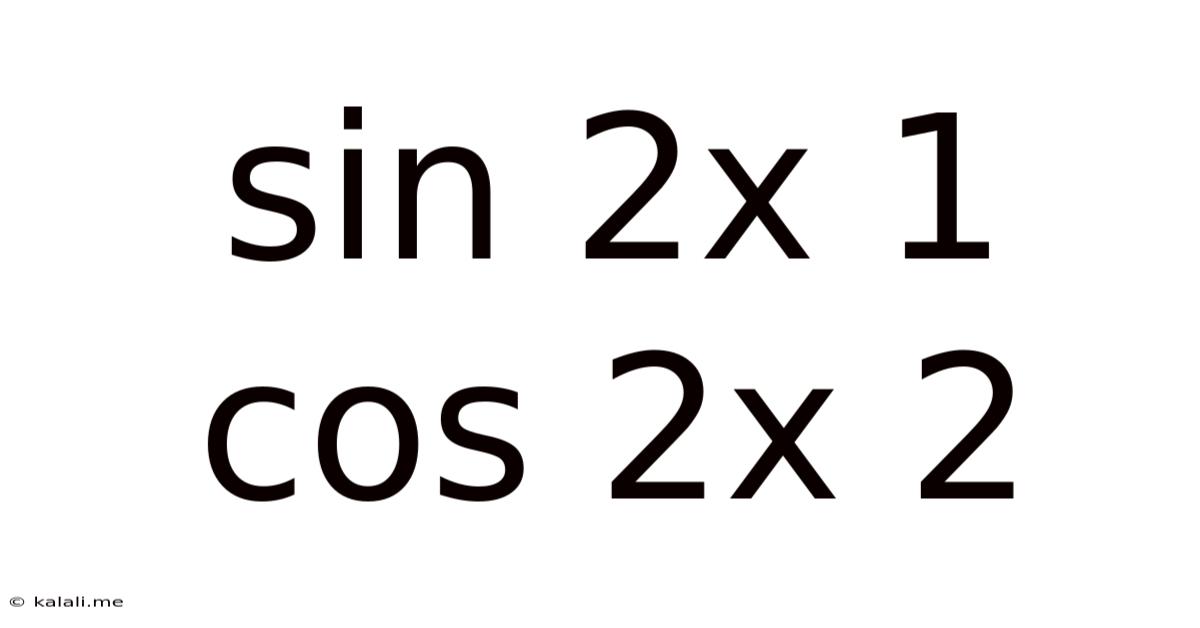
Table of Contents
Understanding and Solving Trigonometric Equations: sin 2x + cos 2x = 2
This article delves into the trigonometric equation sin 2x + cos 2x = 2, exploring its solutions and the underlying mathematical principles. We will examine the nature of trigonometric functions, their periodic properties, and how these properties influence the solution set of such equations. This exploration will equip you with a deeper understanding of trigonometric identities and equation solving techniques.
Understanding the Equation's Components
The equation sin 2x + cos 2x = 2 involves two fundamental trigonometric functions: sine and cosine. Both functions are periodic, meaning their values repeat over a specific interval. The argument '2x' indicates a horizontal compression of the graphs of both sine and cosine, affecting the frequency of their oscillations.
Analyzing the Range of Sine and Cosine
The key to solving this equation lies in understanding the range of sine and cosine functions. Both sine and cosine functions have a range of [-1, 1]. This means that the maximum value either function can attain is 1, and the minimum value is -1.
Solving the Equation: sin 2x + cos 2x = 2
Considering the ranges of sin 2x and cos 2x individually, we find that:
- -1 ≤ sin 2x ≤ 1
- -1 ≤ cos 2x ≤ 1
For the equation sin 2x + cos 2x = 2 to hold true, both sin 2x and cos 2x must simultaneously reach their maximum values. That is:
- sin 2x = 1
- cos 2x = 1
However, this is only possible at specific values of 2x. Let's examine the unit circle to find these points.
Finding the Values of 2x
The sine function equals 1 at 2x = π/2 + 2kπ, where 'k' is any integer. The cosine function equals 1 at 2x = 2nπ, where 'n' is any integer.
For both conditions to be simultaneously true, we require:
- π/2 + 2kπ = 2nπ
Solving for 'k' and 'n', it is apparent there are no integer solutions to this equation where k and n are integers simultaneously satisfy the equation. This means there are no real solutions to the equation sin 2x + cos 2x = 2.
Conclusion
The equation sin 2x + cos 2x = 2 has no real solutions. This is because the maximum value for both sin 2x and cos 2x is 1, and their sum cannot exceed 2 unless they are simultaneously at their maximum value. But this will only happen at different x values simultaneously which make the equation unsolvable. This highlights the importance of considering the range and properties of trigonometric functions when attempting to solve trigonometric equations. Understanding the fundamental principles, such as the range of trigonometric functions, is critical to correctly identifying solvable and unsolvable equations. This provides a foundation for tackling more complex trigonometric problems.
Latest Posts
Latest Posts
-
How Much Is An Acre In Miles
Jul 01, 2025
-
How Much Is 7 8 Of A Cup
Jul 01, 2025
-
5 Letter Words With Y As The Only Vowel
Jul 01, 2025
-
How Long Can A Catfish Live Out Of Water
Jul 01, 2025
-
How Many Cups In 12 Oz Chocolate Chips
Jul 01, 2025
Related Post
Thank you for visiting our website which covers about Sin 2x 1 Cos 2x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.