Smallest Common Multiple Of 3 And 4
Kalali
Mar 30, 2025 · 5 min read
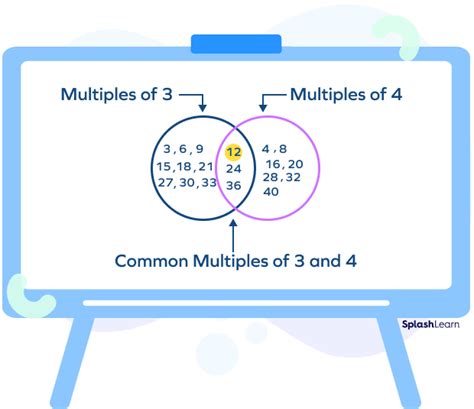
Table of Contents
Finding the Smallest Common Multiple (LCM) of 3 and 4: A Deep Dive
The concept of the least common multiple (LCM) is a fundamental element in number theory and has wide-ranging applications in various fields, from scheduling tasks to simplifying fractions. This article will comprehensively explore the LCM of 3 and 4, examining various methods for calculating it and delving into its significance within mathematical contexts and real-world applications.
Understanding Least Common Multiples
Before we dive into the specifics of finding the LCM of 3 and 4, let's solidify our understanding of the concept itself. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer that is divisible by both 2 and 3.
Key characteristics of the LCM:
- Positive Integer: The LCM is always a positive integer.
- Divisibility: The LCM is divisible by all the numbers in the set.
- Smallest Value: It's the smallest positive integer satisfying the divisibility condition.
Methods for Calculating the LCM of 3 and 4
There are several effective methods to determine the LCM of 3 and 4. We will explore three common approaches: listing multiples, prime factorization, and using the greatest common divisor (GCD).
Method 1: Listing Multiples
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27... Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32...
Observing the lists, we see that the smallest multiple common to both 3 and 4 is 12. Therefore, the LCM(3, 4) = 12.
Method 2: Prime Factorization
This method utilizes the prime factorization of each number. The prime factorization of a number is its representation as a product of prime numbers.
- Prime factorization of 3: 3 (3 is a prime number itself)
- Prime factorization of 4: 2 x 2 = 2²
To find the LCM using prime factorization, we identify the highest power of each prime factor present in either factorization and multiply them together. In this case, we have the prime factors 2 and 3. The highest power of 2 is 2² and the highest power of 3 is 3¹. Therefore:
LCM(3, 4) = 2² x 3 = 4 x 3 = 12
Method 3: Using the Greatest Common Divisor (GCD)
The GCD, or greatest common divisor, is the largest positive integer that divides each of the integers without leaving a remainder. There's a relationship between the LCM and GCD of two numbers (a and b):
LCM(a, b) = (|a x b|) / GCD(a, b)
First, let's find the GCD of 3 and 4. Since 3 and 4 have no common divisors other than 1, their GCD is 1.
Now, we can apply the formula:
LCM(3, 4) = (3 x 4) / GCD(3, 4) = 12 / 1 = 12
Applications of LCM in Real-World Scenarios
The LCM finds practical applications in diverse fields. Here are some examples:
1. Scheduling and Planning
Imagine you have two machines: one completes a cycle every 3 minutes, and the other every 4 minutes. To find the time when both machines will complete a cycle simultaneously, we need to find the LCM of 3 and 4, which is 12. Both machines will complete a cycle together after 12 minutes.
This principle extends to scheduling appointments, coordinating work shifts, and organizing events where multiple recurring activities need synchronization.
2. Fraction Operations
The LCM plays a crucial role in adding and subtracting fractions with different denominators. To add fractions, we find the LCM of the denominators and then express each fraction with the LCM as the new denominator. This allows us to add or subtract the numerators directly.
For example, to add 1/3 and 1/4, we find the LCM of 3 and 4 (which is 12). We then rewrite the fractions as 4/12 and 3/12, respectively, and add them to get 7/12.
3. Music Theory
In music theory, the LCM is used to determine the least common multiple of the durations of different musical notes. This is important for understanding rhythmic patterns and harmonies.
4. Gear Ratios and Rotational Mechanics
In mechanical engineering, the LCM helps calculate gear ratios and determine when two rotating components will be in alignment after a specific number of rotations.
5. Modular Arithmetic and Cryptography
The LCM is a key concept in modular arithmetic, which has applications in cryptography and coding theory. It is crucial for determining cycles and congruences.
Expanding on LCM: More than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For instance, to find the LCM of 3, 4, and 5, we can use prime factorization:
- Prime factorization of 3: 3
- Prime factorization of 4: 2²
- Prime factorization of 5: 5
LCM(3, 4, 5) = 2² x 3 x 5 = 4 x 3 x 5 = 60
Conclusion: The Significance of LCM(3, 4) = 12
The LCM of 3 and 4, which is 12, is a seemingly simple result but represents a fundamental concept with far-reaching implications. Understanding how to calculate LCMs using different methods empowers us to solve a variety of problems in mathematics and various real-world applications, ranging from scheduling tasks to working with fractions and understanding fundamental principles in physics and music. This seemingly simple calculation forms the bedrock of more complex mathematical operations and has a significant impact across numerous disciplines. Mastering the concept of LCM is a crucial step in building a strong foundation in mathematics and problem-solving skills.
Latest Posts
Latest Posts
-
62 C Is What In F
Apr 01, 2025
-
Which Type Of Mutation Stops The Translation Of Mrna
Apr 01, 2025
-
500 Mg Is Equal To How Many Grams
Apr 01, 2025
-
What Is The Percent By Mass Of Sodium In Nacl
Apr 01, 2025
-
Do Swai Have Fins And Scales
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Smallest Common Multiple Of 3 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
