Square Root Of X Divided By X
Kalali
Aug 20, 2025 · 5 min read
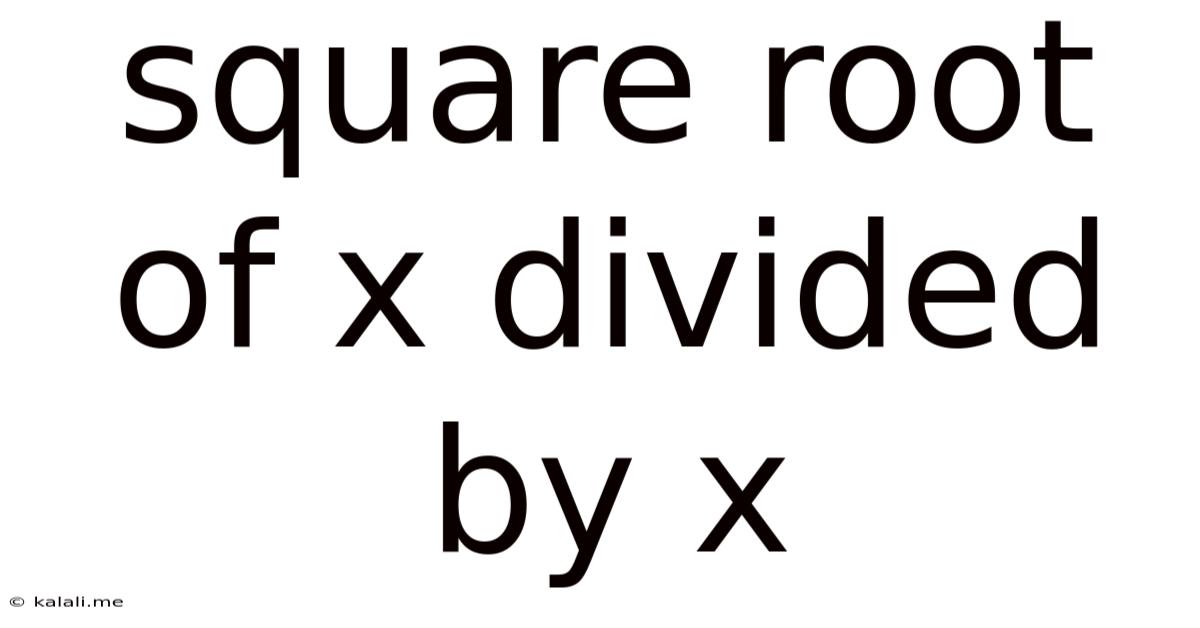
Table of Contents
Decoding the Intriguing Behavior of √x / x: A Deep Dive into Mathematical Analysis and its Applications
The seemingly simple expression √x / x, where x is a positive real number, presents a rich opportunity for mathematical exploration. This article will delve into its properties, analyze its behavior across different domains, explore its applications, and unravel some of its intriguing characteristics. Understanding this expression requires a blend of algebraic manipulation, calculus, and a keen eye for detail. This exploration will be particularly insightful for students of mathematics, engineers, and anyone interested in the intricacies of mathematical functions.
Understanding the Basic Structure and Simplification
At its core, √x / x represents the ratio of the square root of x to x itself. We can simplify this expression using fundamental algebraic rules. Recalling that √x = x<sup>1/2</sup>, we can rewrite the expression as:
x<sup>1/2</sup> / x<sup>1</sup> = x<sup>(1/2 - 1)</sup> = x<sup>-1/2</sup>
This simplification reveals that the expression is equivalent to x raised to the power of -1/2. This is a crucial observation that will underpin much of our subsequent analysis. Alternatively, we can express it as 1/√x or 1/x<sup>1/2</sup>. Each of these forms offers a unique perspective on the function's behavior.
Analyzing the Domain and Range
The domain of the function, meaning the set of all possible input values (x), is crucial to understanding its behavior. Since we are dealing with a square root, x must be non-negative (x ≥ 0) to avoid complex numbers. However, since we're dividing by x, x cannot be zero (x ≠ 0). Therefore, the domain of the function √x / x is (0, ∞), representing all positive real numbers.
The range of the function, the set of all possible output values, can be determined by analyzing the simplified form x<sup>-1/2</sup>. As x approaches infinity, x<sup>-1/2</sup> approaches 0. Conversely, as x approaches 0 from the positive side (0+), x<sup>-1/2</sup> approaches infinity. Therefore, the range of the function is (0, ∞), mirroring its domain.
Investigating the Behavior using Calculus
Calculus provides powerful tools to investigate the behavior of functions more deeply. Let's analyze the function using the first and second derivatives. Recall that our simplified function is f(x) = x<sup>-1/2</sup>.
- First Derivative (f'(x)): The first derivative represents the instantaneous rate of change of the function. Using the power rule of differentiation, we find:
f'(x) = (-1/2)x<sup>(-1/2 - 1)</sup> = (-1/2)x<sup>-3/2</sup> = -1/(2x<sup>3/2</sup>)
Notice that the first derivative is always negative for x > 0. This indicates that the function is always decreasing across its entire domain.
- Second Derivative (f''(x)): The second derivative describes the concavity of the function. Differentiating the first derivative, we get:
f''(x) = (3/4)x<sup>(-3/2 - 1)</sup> = (3/4)x<sup>-5/2</sup> = 3/(4x<sup>5/2</sup>)
The second derivative is always positive for x > 0. This means the function is always concave up, exhibiting a continuously decreasing curve that approaches the x-axis asymptotically.
Graphical Representation and Asymptotic Behavior
Visualizing the function graphically provides further insights. The graph of √x / x will start at infinity when x approaches 0 from the positive side and will asymptotically approach 0 as x approaches infinity. The curve will be continuously decreasing and concave up, reflecting the conclusions drawn from the first and second derivative analysis. This asymptotic behavior is characteristic of many inverse functions and highlights the limiting behavior of the expression as x takes on extreme values.
Applications in Various Fields
The seemingly simple function √x / x finds applications in diverse fields:
-
Physics: In areas like fluid dynamics or electromagnetism, this type of function can model certain decay processes or inversely proportional relationships. For example, the intensity of light decreasing with distance from a source might exhibit a similar trend.
-
Engineering: The function could model the relationship between stress and strain in certain materials under specific conditions, or describe the rate of decay of a signal in communication systems.
-
Economics: In economic models, similar functions can describe the relationship between investment and return, particularly in situations where marginal returns decrease as investment increases. The asymptotic approach to zero suggests diminishing returns.
-
Probability and Statistics: Variations of this function might appear in probability density functions or in the analysis of certain statistical distributions. The decreasing nature of the curve reflects scenarios where the probability of an event decreases with increasing values of a variable.
Comparing to Related Functions
It's beneficial to compare √x / x to related functions to gain a broader perspective:
-
1/x: This function also approaches 0 as x approaches infinity and approaches infinity as x approaches 0 from the positive side. However, 1/x is steeper near x=0 and decreases more rapidly than √x/x.
-
1/√x: This is directly equivalent to √x/x, emphasizing that the expression is essentially an inverse square root function.
-
x<sup>-n</sup> (where n > 0): Our function is a specific case of this broader class of functions. The behavior of these functions shares similarities with our function, illustrating the concept of inverse power functions and their decay characteristics.
Exploring Advanced Concepts and Extensions
Further investigation could involve exploring the function's behavior in the complex plane (allowing for complex values of x), analyzing its integral (calculating the area under the curve), or considering its generalization to higher-order roots (e.g., ³√x / x). These advanced explorations would delve into more complex mathematical tools and uncover even richer insights.
Conclusion: The Unassuming Power of a Simple Expression
While seemingly simple, the expression √x / x reveals a surprising depth when subjected to rigorous mathematical analysis. Its properties, behavior, and applications showcase the interconnectivity of various mathematical concepts. From basic algebraic manipulation to advanced calculus techniques, understanding this function highlights the power of mathematical tools in analyzing and interpreting real-world phenomena. Its asymptotic behavior, always decreasing nature, and concave-up characteristic make it a valuable building block in modeling a wide range of processes across various disciplines. This exploration serves as a testament to the inherent beauty and practical utility found within even the most straightforward mathematical expressions. The journey of exploring √x / x has undoubtedly showcased the multifaceted nature of mathematics and its significant role in shaping our understanding of the world around us.
Latest Posts
Latest Posts
-
How Many Pieces Of Chicken In Kfc Bucket
Aug 20, 2025
-
How Much Do Naked And Afraid Contestants Get Paid
Aug 20, 2025
-
Average Shoe Size For 14 Year Old Girl
Aug 20, 2025
-
How Many Ww Points In An Avocado
Aug 20, 2025
-
What Continent Is At 0 Latitude And 30 East
Aug 20, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of X Divided By X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.