The Intersection Of Two Planes Can Be A Ray.
Kalali
Mar 31, 2025 · 6 min read
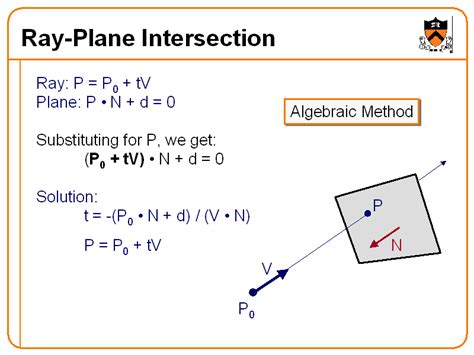
Table of Contents
The Intersection of Two Planes: When a Ray Emerges
The intersection of two planes in three-dimensional space is a fundamental concept in geometry and linear algebra. While many visualize the intersection as a line, a less commonly considered possibility is that the intersection can be a ray. This subtle but crucial distinction highlights the importance of carefully examining the conditions under which such an intersection occurs. This article delves into the mathematical principles behind plane intersections, specifically exploring the scenarios where a ray, rather than a full line, forms the intersection. We will explore the conditions, provide illustrative examples, and discuss the implications within various applications.
Understanding Plane Equations
Before exploring ray intersections, let's solidify our understanding of plane equations. A plane in 3D space can be defined by a point on the plane and a vector normal (perpendicular) to the plane. The equation of a plane is typically represented in the form:
Ax + By + Cz + D = 0
where A, B, and C are the components of the normal vector, and D is a constant determined by the position of the plane relative to the origin. Different forms of this equation exist, such as the point-normal form and the intercept form, but the standard form above serves as a robust foundation for our discussion.
The Line of Intersection: The Usual Case
When two planes intersect, they typically do so along a straight line. This line can be parameterized using a vector equation:
r(t) = r₀ + tv
where:
- r(t) is a point on the line, parameterized by the scalar t.
- r₀ is a known point on the line (found by solving the system of plane equations).
- v is a vector parallel to the line (found by taking the cross product of the normal vectors of the two planes).
This line extends infinitely in both directions. Finding this line involves solving the system of two linear equations in three variables, representing the equations of the two planes.
Finding the Line of Intersection: A Worked Example
Let's consider two planes:
Plane 1: 2x + y - z = 5 Plane 2: x - y + 2z = 2
To find the line of intersection, we can solve this system of equations. One common approach is to express one variable (e.g., x) in terms of another (e.g., y) and then parameterize the result. From Plane 1, we can express z as:
z = 2x + y - 5
Substitute this into Plane 2:
x - y + 2(2x + y - 5) = 2
Simplifying, we get:
5x + y = 12
Solving for y, we have:
y = 12 - 5x
Now, substituting this back into the expression for z:
z = 2x + (12 - 5x) - 5 = -3x + 7
Therefore, we can parameterize the line of intersection as:
x = t y = 12 - 5t z = 7 - 3t
This represents a line extending infinitely in both directions.
The Ray Intersection: A Special Case
The intersection becomes a ray when the planes intersect along a line but we impose a boundary condition that limits the line's extent in one direction. This boundary condition can arise from various constraints, including:
- Physical constraints: Imagine two planes representing physical surfaces; the intersection might be limited by the edges of these surfaces, creating a ray.
- Domain restrictions: In certain applications (e.g., optimization problems, computer graphics), the domain of the variables might be restricted, effectively truncating the line of intersection to form a ray.
- Inequalities: Introducing inequalities related to the plane equations can create half-spaces, and the intersection of these half-spaces with the line of intersection could result in a ray.
Visualizing a Ray Intersection
Consider two planes intersecting at a line, but imagine one plane is partially obscured or truncated. Only a segment of the line resulting from the intersection of the complete planes will be visible, forming a ray. The ray's endpoint is determined by the boundary imposed by the truncation or constraint.
Mathematical Representation of a Ray
A ray can be represented mathematically as:
r(t) = r₀ + tv, t ≥ 0
The key difference from the line equation is the added constraint t ≥ 0. This signifies that the ray originates at r₀ and extends infinitely only in one direction defined by the vector v.
Examples of Ray Intersections
-
Planes with Limited Extent: Imagine two physical walls intersecting. The intersection is a line only if the walls are infinitely long. In reality, the walls have finite length, so the intersection is a ray. The endpoint of the ray would be at the point where either wall ends.
-
Domain Constraints: Consider an optimization problem where the variables x, y, and z must be non-negative. If the line of intersection of two planes passes through the region where x, y, and z are all non-negative, the intersection in this restricted domain is a ray. The origin is a natural endpoint of this ray.
-
Half-spaces defined by inequalities: The intersection of the half-spaces defined by 2x + y - z ≥ 5 and x - y + 2z ≤ 2 could, depending on the specific configuration of the planes, result in a ray as the solution.
Applications and Implications
The concept of a ray intersection holds significance in various fields:
- Computer Graphics: Ray tracing algorithms rely heavily on the intersection of rays with surfaces (represented as planes or more complex shapes). Understanding ray intersections is critical for realistic rendering.
- Robotics: Path planning for robots often involves determining the intersection of the robot's workspace (represented by planes or other geometric shapes) and its planned trajectory (represented by rays or lines).
- Physics: In optics, the propagation of light can be modeled using rays. The intersection of light rays with surfaces governs phenomena like reflection and refraction.
- Linear Programming: The feasible region in linear programming problems is often defined by a system of inequalities, which might lead to feasible regions with boundary segments representing rays.
Conclusion
While the typical intersection of two planes is a line, the possibility of a ray intersection is crucial and should not be overlooked. By understanding the conditions that lead to a ray (constraints, limited domain, half-spaces), we can accurately model and solve problems in various fields where plane intersections play a significant role. Careful consideration of these scenarios ensures a thorough and accurate understanding of geometric relationships in three-dimensional space and their application in real-world problems. Further exploration could delve into specific applications like shadow generation in computer graphics or finding feasible solutions within the confines of optimization problems – showcasing the versatility and importance of understanding ray intersections as a distinct subset of plane intersection analysis. The detailed exploration of various boundary conditions and their impact on the nature of the intersection remains a fertile area for further investigation and expands the practical applications of this fundamental geometric principle.
Latest Posts
Latest Posts
-
40 Oz Of Water Is How Many Cups
Jul 18, 2025
-
How Many Eighths In A Quarter Pound
Jul 18, 2025
-
Can The Sine Of An Angle Ever Equal 2
Jul 18, 2025
-
How Many Months Is A Hundred Days
Jul 18, 2025
-
Mother And I Or Mother And Me
Jul 18, 2025
Related Post
Thank you for visiting our website which covers about The Intersection Of Two Planes Can Be A Ray. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.