The Polynomial 2x3-5x2 4x-10 Is Split Into Two Groups
Kalali
Apr 02, 2025 · 5 min read
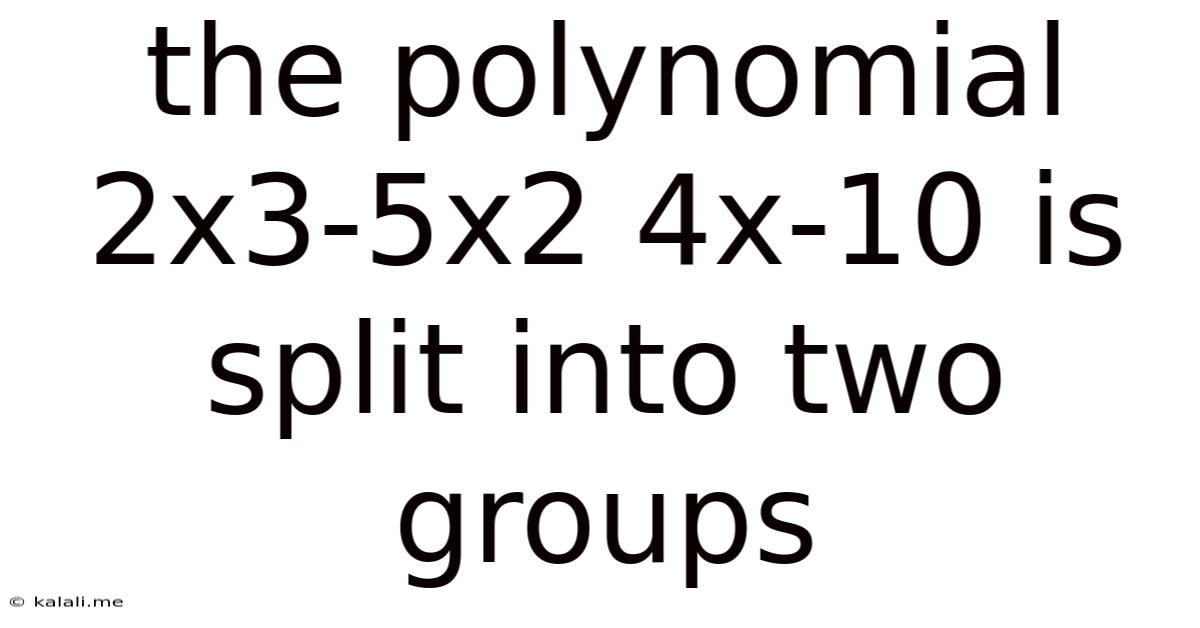
Table of Contents
Exploring the Polynomial 2x³ - 5x² + 4x - 10: A Deep Dive into Grouping and Factorization
The polynomial 2x³ - 5x² + 4x - 10 presents a fascinating case study in algebraic manipulation and factorization techniques. While seemingly simple at first glance, its structure allows us to explore multiple approaches, highlighting the power and flexibility of algebraic tools. This article delves into the intricacies of grouping this polynomial, examining various factorization methods and discussing the underlying mathematical concepts. We'll uncover the significance of grouping, its limitations, and how it relates to other factorization strategies.
Understanding Polynomial Factorization
Before we dive into the specifics of 2x³ - 5x² + 4x - 10, let's establish a foundational understanding of polynomial factorization. Factorization, in essence, is the process of expressing a polynomial as a product of simpler polynomials. This process is crucial in various mathematical applications, including solving equations, simplifying expressions, and understanding the behavior of functions.
There are several methods for factoring polynomials, including:
- Greatest Common Factor (GCF): This involves identifying the largest common factor among all terms and factoring it out.
- Difference of Squares: This technique applies to binomials of the form a² - b², which factors as (a + b)(a - b).
- Sum/Difference of Cubes: Similar to the difference of squares, this handles expressions of the form a³ + b³ and a³ - b³.
- Grouping: This method involves grouping terms with common factors to facilitate factorization. This is the technique we will focus on for 2x³ - 5x² + 4x - 10.
- Quadratic Formula: For quadratic polynomials (degree 2), the quadratic formula provides a direct method for finding roots and hence factors.
- Rational Root Theorem: This theorem helps identify potential rational roots of a polynomial, which can then be used to find factors.
Grouping the Polynomial 2x³ - 5x² + 4x - 10
The method of grouping involves strategically partitioning the polynomial into groups of terms that share common factors. For 2x³ - 5x² + 4x - 10, we can group the terms as follows:
(2x³ - 5x²) + (4x - 10)
Now, we factor out the GCF from each group:
x²(2x - 5) + 2(2x - 5)
Notice that both terms now share the common factor (2x - 5). We can factor this out:
(2x - 5)(x² + 2)
This is the factored form of the polynomial 2x³ - 5x² + 4x - 10 using the grouping method. This demonstrates that the polynomial can be expressed as the product of a linear factor (2x - 5) and a quadratic factor (x² + 2).
Analyzing the Factors
Let's examine the factors we obtained:
-
(2x - 5): This is a linear factor. Setting this factor to zero gives us the root x = 5/2. This is a real root.
-
(x² + 2): This is a quadratic factor. To find its roots, we set it to zero:
x² + 2 = 0
x² = -2
x = ±√(-2) = ±i√2
These are complex roots (involving the imaginary unit 'i').
Significance of the Factorization
The factorization of 2x³ - 5x² + 4x - 10 into (2x - 5)(x² + 2) reveals important information about the polynomial:
-
Roots: We identified one real root (x = 5/2) and two complex roots (x = ±i√2). The Fundamental Theorem of Algebra states that a polynomial of degree n has exactly n roots (counting multiplicity and including complex roots). Our cubic polynomial has three roots, as expected.
-
Behavior of the Function: The factorization helps us understand the behavior of the function f(x) = 2x³ - 5x² + 4x - 10. The real root indicates that the graph of the function intersects the x-axis at x = 5/2. The complex roots don't directly correspond to x-intercepts on the real number plane.
Alternative Approaches to Factorization
While grouping proved successful in this case, it's important to note that other factorization methods might also be applicable, depending on the polynomial's structure. For instance, if we suspected rational roots, we could have used the Rational Root Theorem to test potential rational roots and then perform polynomial long division to find other factors.
The Rational Root Theorem states that any rational root of a polynomial with integer coefficients must be of the form p/q, where p is a factor of the constant term and q is a factor of the leading coefficient. In our case, the constant term is -10 and the leading coefficient is 2. Therefore, potential rational roots would include ±1, ±2, ±5, ±10, ±1/2, ±5/2. Testing these, we would find x = 5/2 as a root, confirming the factor (2x - 5).
Limitations of Grouping
While grouping is a powerful tool, it's not always guaranteed to work. The success of grouping depends heavily on the arrangement of terms and the presence of common factors. If a polynomial cannot be readily grouped into factors with common terms, alternative methods like the Rational Root Theorem or more advanced techniques (like solving cubic equations directly) may be necessary.
Extending the Concept: Applications of Polynomial Factorization
Polynomial factorization is far from a purely theoretical exercise. It has widespread applications across various fields, including:
- Calculus: Finding roots of polynomials is essential in analyzing the critical points and behavior of functions.
- Engineering: Polynomial functions are frequently used to model physical phenomena, and factorization helps simplify and analyze these models.
- Computer Science: Polynomial factorization plays a role in cryptography and algorithm design.
- Statistics: Polynomial regression models use polynomials to fit data, and factorization helps interpret these models.
Conclusion: The Power and Versatility of Polynomial Factorization
The seemingly straightforward polynomial 2x³ - 5x² + 4x - 10 provided a valuable opportunity to explore the intricacies of polynomial factorization, specifically focusing on the grouping method. We successfully factored the polynomial, revealing its roots and providing insights into its behavior. However, the exploration highlighted the importance of understanding multiple factorization techniques and their limitations. The ability to effectively factor polynomials is a fundamental skill with broad applications across diverse fields, underscoring its significance in mathematics and beyond. This detailed analysis serves not only to solve the specific problem of factoring this cubic polynomial but also to equip readers with a deeper understanding of the broader concepts and techniques involved in polynomial manipulation. Understanding the strengths and weaknesses of various methods ensures a flexible and adaptable approach to solving future algebraic problems.
Latest Posts
Latest Posts
-
True Or False Prehistoric Humans Felt Stress
Apr 03, 2025
-
120 Out Of 150 As A Percentage
Apr 03, 2025
-
Cuanto Son 40 Onzas En Litros
Apr 03, 2025
-
What Is 19 Out Of 25
Apr 03, 2025
-
Cuantos Grados Son 64 Fahrenheit En Centigrados
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about The Polynomial 2x3-5x2 4x-10 Is Split Into Two Groups . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
