Thirty Six And Nine Thousandths As A Decimal
Kalali
Jul 02, 2025 · 5 min read
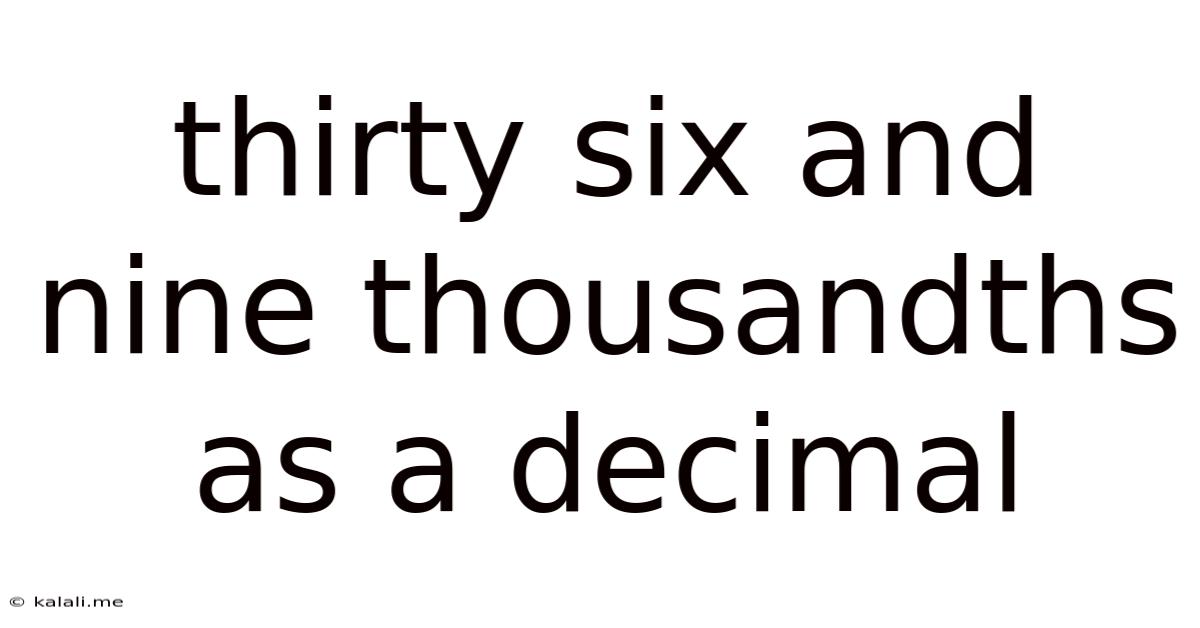
Table of Contents
Thirty-Six and Nine Thousandths as a Decimal: A Comprehensive Guide
Understanding how to represent numbers in different formats is a fundamental skill in mathematics. This article delves deep into the representation of "thirty-six and nine thousandths" as a decimal, exploring the underlying concepts, providing multiple approaches to solving this, and expanding on related decimal concepts for a complete understanding. This guide is designed to help students, educators, and anyone seeking a clearer grasp of decimal numbers.
What is a Decimal Number?
Before we jump into converting "thirty-six and nine thousandths" to a decimal, let's refresh our understanding of what decimal numbers are. A decimal number is a way of writing a number that includes a fractional part, separated from the whole number part by a decimal point (.). The digits to the left of the decimal point represent whole numbers, while the digits to the right represent fractions of a whole. Each position to the right of the decimal point represents a decreasing power of 10. The first position is tenths (1/10), the second is hundredths (1/100), the third is thousandths (1/1000), and so on.
Understanding Place Value
Understanding place value is crucial for converting numbers from words to decimals. Let's analyze the number "thirty-six and nine thousandths":
-
Thirty-six: This represents the whole number part of our number. It signifies 3 tens and 6 ones, or 30 + 6 = 36.
-
And: This word indicates the separation between the whole number part and the fractional part. It's where the decimal point will be placed.
-
Nine thousandths: This is the fractional part. It signifies 9 parts out of 1000.
Converting "Thirty-Six and Nine Thousandths" to a Decimal
Now, let's combine our understanding to convert the number into its decimal form:
-
Write the whole number: We start by writing the whole number part, which is 36.
-
Add the decimal point: After the whole number, we add a decimal point (.). This separates the whole number from the fractional part.
-
Write the fractional part: The fractional part is "nine thousandths," meaning 9/1000. Since the denominator is 1000, we know we need three digits to the right of the decimal point to represent the thousandths place. Therefore, we write 009 after the decimal point. The leading zeros are important to maintain the correct place value.
Therefore, "thirty-six and nine thousandths" as a decimal is 36.009.
Alternative Approaches and Deeper Understanding
While the above method is straightforward, let's explore other ways to approach this conversion, further solidifying our understanding:
-
Fraction to Decimal Conversion: We can first represent "nine thousandths" as a fraction: 9/1000. Then, we can perform the division: 9 ÷ 1000 = 0.009. Finally, we combine this with the whole number part: 36 + 0.009 = 36.009. This approach emphasizes the relationship between fractions and decimals.
-
Expanded Form: Writing the number in expanded form helps visualize the place value of each digit: (3 x 10) + (6 x 1) + (9 x 0.001) = 30 + 6 + 0.009 = 36.009. This method reinforces the concept of place value.
Common Mistakes and How to Avoid Them
Several common mistakes can occur when converting numbers from words to decimals. Being aware of these pitfalls can help ensure accuracy:
-
Incorrect placement of the decimal point: Carefully identify the "and," which indicates the separation between the whole and fractional parts. The decimal point should be placed immediately after the whole number.
-
Missing leading zeros: When the fractional part has fewer digits than the denominator suggests (e.g., thousandths requiring three digits), ensure you include leading zeros to maintain the correct place value. For example, "nine hundredths" should be written as 0.09, not .09 or .9.
-
Confusing tenths, hundredths, and thousandths: Thoroughly understand the place value system. Remember that each place to the right of the decimal point represents a power of ten: tenths (1/10), hundredths (1/100), thousandths (1/1000), ten-thousandths (1/10000), and so on.
Expanding on Decimal Concepts
Let's expand our understanding of decimals by exploring some related concepts:
-
Rounding Decimals: Rounding decimals involves approximating a number to a certain number of decimal places. For example, rounding 36.009 to one decimal place would result in 36.0. Rounding to two decimal places would still be 36.01.
-
Comparing Decimals: Comparing decimals requires careful attention to place value. For example, 36.009 is smaller than 36.01 because the hundredths place is decisive.
-
Adding and Subtracting Decimals: Adding and subtracting decimals requires aligning the decimal points vertically before performing the operation.
-
Multiplying and Dividing Decimals: Multiplying decimals involves multiplying the numbers as if they were whole numbers and then placing the decimal point based on the total number of decimal places in the original numbers. Dividing decimals involves moving the decimal point in both the dividend and divisor until the divisor is a whole number before performing the division.
Practical Applications of Decimals
Decimals are used extensively in various real-world scenarios:
-
Finance: Money is often expressed using decimals (e.g., $36.009).
-
Measurement: Measurements like length, weight, and volume are often represented using decimals (e.g., 36.009 meters).
-
Science: Scientific data and calculations often involve decimals.
-
Technology: Computer programming and digital displays frequently utilize decimals.
Conclusion
Converting "thirty-six and nine thousandths" to its decimal equivalent, 36.009, is a fundamental skill built upon a solid understanding of place value and decimal representation. By mastering this concept and exploring related decimal operations, we strengthen our mathematical abilities and develop valuable skills applicable across numerous fields. Remember to practice regularly, focusing on avoiding common mistakes to build confidence and fluency. The more you work with decimals, the more intuitive they will become.
Latest Posts
Latest Posts
-
How Many Times Does 3 Go Into 48
Jul 31, 2025
-
Early Blues Recordings Were Categorized In Which Two Ways
Jul 31, 2025
-
Does Giant Eagle Sell Liquor On Sundays
Jul 31, 2025
-
Is 33 A Prime Number Or A Composite Number
Jul 31, 2025
-
Gallons Per Minute To Pounds Per Hour
Jul 31, 2025
Related Post
Thank you for visiting our website which covers about Thirty Six And Nine Thousandths As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.