Twice A Number Plus 4 Is 8
Kalali
Jul 28, 2025 · 5 min read
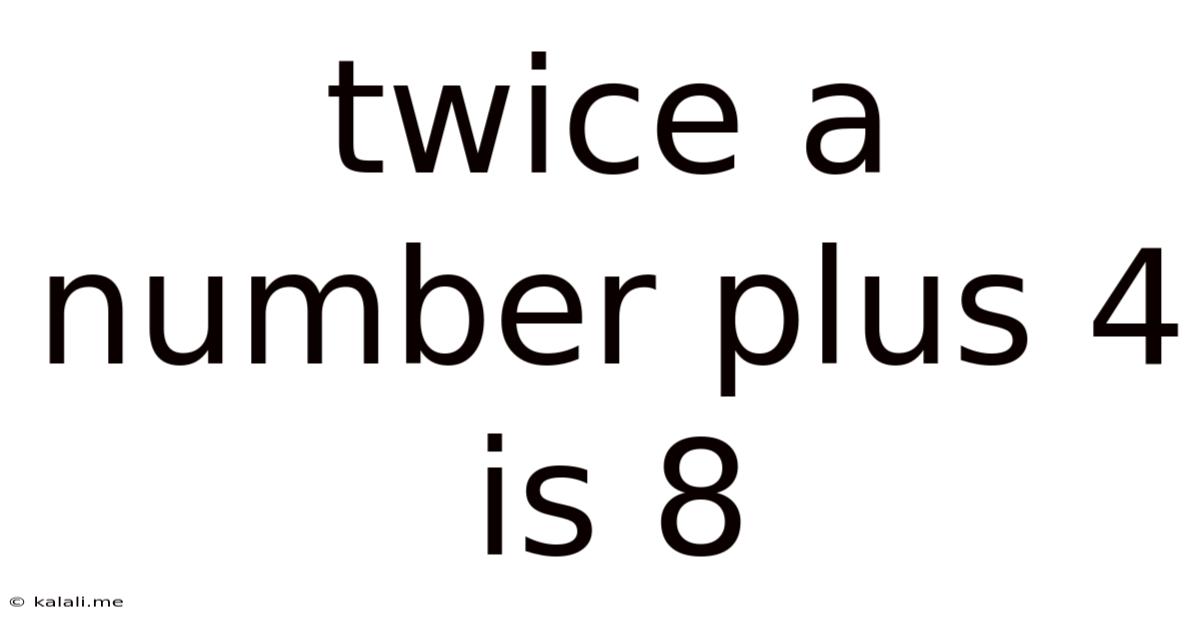
Table of Contents
Twice a Number Plus 4 is 8: Unpacking a Simple Equation and its Broader Implications
This seemingly simple mathematical statement, "Twice a number plus 4 is 8," hides a wealth of concepts within its concise phrasing. It's a gateway to understanding fundamental algebraic principles, problem-solving strategies, and even the broader applications of mathematics in everyday life. This article will delve deep into this seemingly simple equation, exploring its solution, its variations, and its significance in the wider mathematical landscape.
Meta Description: Learn how to solve the algebraic equation "Twice a number plus 4 is 8," explore various problem-solving methods, and discover its applications in real-world scenarios. This comprehensive guide unravels the underlying mathematical principles and expands on related concepts.
Understanding the Equation: Breaking Down the Components
The statement "Twice a number plus 4 is 8" can be translated directly into an algebraic equation. Let's break down the components:
- "Twice a number": This translates to 2x, where 'x' represents the unknown number. Multiplication is implied by the word "twice."
- "Plus 4": This signifies adding 4 to the previous expression, resulting in 2x + 4.
- "Is 8": This indicates that the entire expression is equal to 8, giving us the complete equation: 2x + 4 = 8.
This simple equation exemplifies the fundamental structure of many algebraic problems: an unknown variable (x), constants (4 and 8), and operations (+ and =).
Solving the Equation: Unveiling the Unknown
Solving the equation 2x + 4 = 8 involves isolating the variable 'x' to determine its value. We can achieve this using several methods, all based on the principles of maintaining equality on both sides of the equation.
Method 1: Subtraction and Division
This is perhaps the most straightforward approach. We first subtract 4 from both sides of the equation to isolate the term with 'x':
2x + 4 - 4 = 8 - 4
This simplifies to:
2x = 4
Next, we divide both sides by 2 to solve for 'x':
2x / 2 = 4 / 2
Therefore:
x = 2
Method 2: Using Inverse Operations
This method emphasizes the concept of inverse operations. Since 4 is added to 2x, we perform the inverse operation—subtraction—to remove it. Similarly, since 'x' is multiplied by 2, we use the inverse operation—division—to isolate 'x'. This method reinforces the fundamental principle that performing the same operation on both sides of an equation maintains its balance.
Verifying the Solution: Checking Our Work
It's crucial to verify our solution by substituting the value of x (which we found to be 2) back into the original equation:
2(2) + 4 = 8
4 + 4 = 8
8 = 8
Since the equation holds true, our solution, x = 2, is correct. This verification step is essential in ensuring the accuracy of our mathematical calculations.
Expanding the Concept: Variations and Extensions
The basic equation "2x + 4 = 8" serves as a foundation for understanding more complex algebraic problems. Let's explore some variations:
1. Changing the Constants:
We can alter the constants (4 and 8) to create different equations, such as:
- 2x + 6 = 10
- 2x + 1 = 5
- 2x + 12 = 20
Solving these equations follows the same principles as the original, involving subtraction and division. The solution will differ depending on the chosen constants.
2. Introducing Negative Numbers:
The equation can also involve negative numbers:
- 2x - 4 = 8
- 2x + 4 = -8
- -2x + 4 = 8
Solving these variations requires careful attention to the rules of signed numbers. For instance, in the equation 2x - 4 = 8, we would first add 4 to both sides before dividing by 2.
3. Equations with Multiple Variables:
While our original equation focuses on one variable, the principles can extend to equations with multiple variables. For example:
2x + y = 8
In this case, we need additional information (another equation relating x and y) to solve for both variables. This introduces the concept of systems of equations, a crucial topic in algebra.
4. More Complex Equations:
The foundation laid by this simple equation is vital for tackling more complicated algebraic expressions involving higher powers of x (e.g., x², x³), different operations, or multiple variables. Understanding this basic equation builds the necessary skills and conceptual understanding for more complex mathematical challenges.
Real-World Applications: Connecting Math to Life
While this equation may seem abstract, its principles have countless real-world applications:
-
Calculating Costs: Imagine you are buying items that cost twice a certain amount, plus a fixed fee (like a delivery charge). The equation helps determine the cost based on the price of individual items.
-
Measuring Quantities: If you know a quantity is twice another plus a constant, this equation allows you to solve for the unknown quantity. This could apply to measuring ingredients in recipes, calculating distances, or many other applications.
-
Financial Planning: Simple interest calculations involve similar mathematical principles. Understanding this type of equation lays the groundwork for understanding compound interest, investment growth, and other financial concepts.
Pedagogical Significance: Building Mathematical Intuition
The equation "Twice a number plus 4 is 8" is exceptionally valuable for teaching fundamental algebraic concepts:
-
Introduction to Variables: The equation introduces the crucial concept of using variables to represent unknown quantities. This is a cornerstone of algebra and its applications in higher-level mathematics and other disciplines.
-
Understanding Equality: The equation emphasizes the importance of maintaining equality on both sides of an equation. Any operation performed on one side must be replicated on the other to preserve the balance.
-
Developing Problem-Solving Skills: Solving this equation demonstrates a fundamental problem-solving approach: breaking down a problem into smaller, manageable steps, performing necessary operations, and verifying the solution.
Conclusion: A Simple Equation with Deep Implications
The seemingly trivial equation, "Twice a number plus 4 is 8," serves as a powerful illustration of fundamental algebraic principles and problem-solving strategies. Its simplicity masks its significant role in building a solid foundation in mathematics, fostering critical thinking skills, and demonstrating the practical applications of math in various aspects of daily life. Mastering this seemingly basic equation opens doors to understanding more complex mathematical concepts and confidently tackling more challenging problems in the future. The ability to translate word problems into algebraic expressions and solve them is a cornerstone of mathematical literacy, essential for success in numerous academic and professional pursuits.
Latest Posts
Latest Posts
-
How Do You Write 80 As A Decimal
Jul 28, 2025
-
How Many Square Miles Is 200 000 Acres
Jul 28, 2025
-
What Is 0 8 Inches On A Ruler
Jul 28, 2025
-
Greatest Common Factor Of 8 And 14
Jul 28, 2025
-
How Many Tablespoons In A Block Of Cream Cheese
Jul 28, 2025
Related Post
Thank you for visiting our website which covers about Twice A Number Plus 4 Is 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.