Un Triángulo Equilátero Es También Un Triángulo
Kalali
Apr 01, 2025 · 5 min read
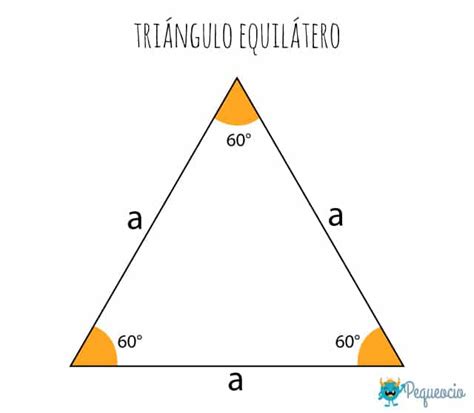
Table of Contents
An Equilateral Triangle is Also a Triangle: Exploring the Properties and Hierarchy of Triangles
An equilateral triangle, with its elegant symmetry and unique properties, is a fascinating geometric shape. Understanding its characteristics requires a firm grasp of the broader category to which it belongs: the triangle. This article delves deep into the properties of triangles, focusing on the equilateral triangle as a specific and important subset. We'll explore their similarities and differences, highlighting why the statement "an equilateral triangle is also a triangle" is fundamentally true and offers crucial insights into geometric relationships.
Understanding the Triangle: A Foundation in Geometry
A triangle, at its most basic, is a polygon with three sides and three angles. This simple definition belies the rich diversity and complex properties embedded within this fundamental shape. Triangles are ubiquitous in geometry, architecture, and nature, their structure appearing in everything from the trusses of bridges to the crystalline formations of minerals. The sum of the interior angles of any triangle always equals 180 degrees – a cornerstone principle in Euclidean geometry.
Classifying Triangles: Exploring the Hierarchy
Triangles are categorized based on two key features: their side lengths and their angles.
1. Classification by Side Lengths:
- Equilateral Triangle: All three sides are of equal length. This is the focus of our exploration today.
- Isosceles Triangle: At least two sides are of equal length.
- Scalene Triangle: All three sides are of different lengths.
2. Classification by Angles:
- Acute Triangle: All three angles are acute (less than 90 degrees).
- Right Triangle: One angle is a right angle (exactly 90 degrees).
- Obtuse Triangle: One angle is obtuse (greater than 90 degrees).
It's crucial to note that these classifications are not mutually exclusive. For example, an equilateral triangle is also an acute triangle because the equal side lengths necessitate equal angles, all of which must be 60 degrees (180°/3 = 60°). This overlap highlights the hierarchical nature of triangle classification.
The Equilateral Triangle: A Special Case
The equilateral triangle stands out as a particularly symmetrical and well-behaved type of triangle. Its defining characteristic – equal side lengths – leads to a cascade of other unique properties:
- Equal Angles: As mentioned, all three angles are equal and measure 60 degrees.
- Altitude, Median, Perpendicular Bisector, and Angle Bisector Coincidence: In an equilateral triangle, the altitude (height) from any vertex to the opposite side, the median (line segment from a vertex to the midpoint of the opposite side), the perpendicular bisector (line segment perpendicular to and bisecting a side), and the angle bisector (line segment bisecting an angle) are all the same line segment. This property simplifies many geometric calculations and constructions.
- Incenter, Circumcenter, Centroid, and Orthocenter Coincidence: The points of concurrency for these four important centers (incenter – center of inscribed circle; circumcenter – center of circumscribed circle; centroid – center of mass; orthocenter – intersection of altitudes) all coincide in an equilateral triangle. This remarkable feature showcases the high degree of symmetry inherent in this special type of triangle.
- Rotational Symmetry: An equilateral triangle exhibits rotational symmetry of order 3. This means it can be rotated by 120 degrees about its center and still appear unchanged.
- Reflectional Symmetry: It possesses three lines of reflectional symmetry – one through each vertex and the midpoint of the opposite side.
Why "An Equilateral Triangle is Also a Triangle" is a Fundamental Truth
The statement "an equilateral triangle is also a triangle" might seem trivially obvious, but it underscores a crucial principle in mathematical classification: subset inclusion. The set of equilateral triangles is a subset of the larger set of all triangles. Every equilateral triangle satisfies the definition of a triangle (three sides, three angles, sum of angles equals 180 degrees), but not every triangle is an equilateral triangle.
This hierarchical relationship is essential for understanding geometric concepts. When we prove theorems about triangles in general, these theorems automatically apply to equilateral triangles as a special case. However, theorems proven for equilateral triangles may not hold true for all triangles. For instance, the property of equal angles only applies to equilateral triangles within the broader category of triangles.
Applications of Equilateral Triangles: From Geometry to Architecture
The unique properties of equilateral triangles make them incredibly useful in various applications:
- Tessellations: Equilateral triangles can perfectly tessellate (tile) a plane, forming a regular hexagonal pattern. This property is evident in honeycomb structures created by bees, demonstrating the efficiency and stability of this geometric arrangement in nature.
- Architecture and Engineering: The equilateral triangle's inherent strength and stability make it a popular choice in structural design. Many bridges and buildings incorporate equilateral triangles in their frameworks to distribute weight effectively.
- Art and Design: The aesthetic appeal of equilateral triangles is exploited in various art forms and design elements. Its balanced and symmetrical nature contributes to visually pleasing compositions.
- Computer Graphics and Game Development: The simplicity and predictable properties of equilateral triangles make them efficient building blocks for creating complex 3D models and game environments.
Advanced Concepts and Related Theorems
The equilateral triangle's simplicity belies its deep connections to more advanced mathematical concepts:
- Trigonometry: The trigonometric ratios (sine, cosine, tangent) for the angles in an equilateral triangle are easily calculated, serving as a foundation for understanding trigonometry.
- Complex Numbers: Equilateral triangles can be represented and analyzed using complex numbers, which opens up advanced geometrical insights.
- Group Theory: The symmetries of an equilateral triangle can be studied using group theory, a branch of abstract algebra.
Conclusion: The Significance of Understanding the Hierarchical Relationship
The understanding that an equilateral triangle is a triangle is fundamental to grasping the interconnectedness of geometric concepts. This hierarchical structure allows us to leverage general properties of triangles while appreciating the specific characteristics that make equilateral triangles unique. Their elegant symmetry, remarkable properties, and wide-ranging applications highlight the significance of this special subset within the broader world of triangles. By recognizing this fundamental relationship, we unlock deeper insights into the beauty and power of geometric forms. The exploration of equilateral triangles, therefore, is not just an exercise in geometry; it’s a journey into the heart of mathematical structure and its elegant applications in the world around us. Further study of these properties will continue to reveal new and exciting applications in various fields, showcasing the enduring relevance of this seemingly simple yet profound geometric shape.
Latest Posts
Latest Posts
-
How Many Ml Is 1 4 Oz
Apr 02, 2025
-
How Many Centimeters Is 23 Inches
Apr 02, 2025
-
How Many Gallons Is 10 Cups
Apr 02, 2025
-
What Is 62 Degrees Celsius In Fahrenheit
Apr 02, 2025
-
Is Usa In The Northern Hemisphere
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Un Triángulo Equilátero Es También Un Triángulo . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
