Unit 3 Power Polynomials And Rational Functions
Kalali
Mar 30, 2025 · 6 min read
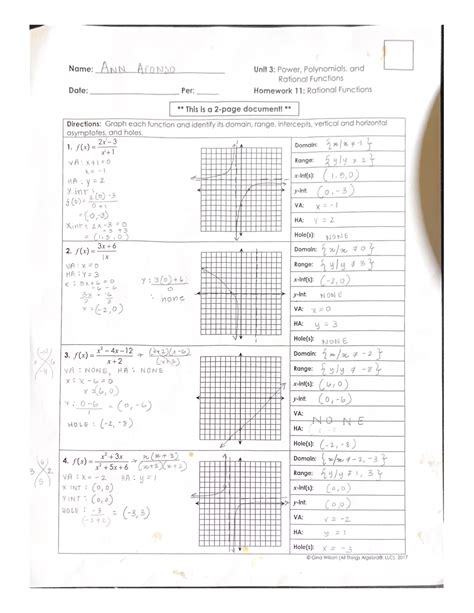
Table of Contents
Unit 3: Power Polynomials and Rational Functions: A Comprehensive Guide
This unit delves into the fascinating world of power polynomials and rational functions, exploring their properties, graphs, and applications. We'll cover key concepts, providing a solid foundation for further mathematical studies.
Understanding Polynomials
A polynomial is an expression consisting of variables (often denoted as 'x') and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents. The general form of a polynomial is:
a_nx^n + a_{n-1}x^{n-1} + ... + a_2x^2 + a_1x + a_0
Where:
a_n, a_{n-1}, ..., a_0are the coefficients (constants).nis a non-negative integer, representing the degree of the polynomial.xis the variable.
Examples of Polynomials:
3x² + 2x - 5(Quadratic polynomial, degree 2)x³ - 7x + 1(Cubic polynomial, degree 3)5x(Linear polynomial, degree 1)7(Constant polynomial, degree 0)
Degree of a Polynomial and its Significance
The degree of a polynomial is the highest power of the variable present in the expression. The degree significantly impacts the polynomial's behavior and graph:
- Linear Polynomials (Degree 1): These represent straight lines.
- Quadratic Polynomials (Degree 2): These represent parabolas (U-shaped curves).
- Cubic Polynomials (Degree 3): These can have up to two turning points.
- Higher-Degree Polynomials: The complexity of the graph increases with the degree, potentially exhibiting multiple turning points and intersections with the x-axis.
Operations with Polynomials
Polynomials can be added, subtracted, multiplied, and divided. These operations are fundamental to manipulating and solving polynomial equations.
- Addition and Subtraction: Combine like terms (terms with the same variable and exponent).
- Multiplication: Use the distributive property (FOIL method for binomials) to expand the expression.
- Division: Long division or synthetic division are used to divide polynomials. The result can be expressed as a quotient and a remainder.
Power Functions: A Special Case of Polynomials
A power function is a specific type of polynomial where the expression is of the form f(x) = ax^n, where 'a' is a constant and 'n' is a positive integer. Power functions form the building blocks for understanding the behavior of more complex polynomials.
Analyzing Power Functions
The graph of a power function is significantly affected by the exponent 'n':
- Even Exponents (n=2, 4, 6,...): The graph is symmetric about the y-axis, resembling a parabola if n=2, with flatter or steeper curves for higher even exponents. The function is always non-negative.
- Odd Exponents (n=1, 3, 5,...): The graph is symmetric about the origin. It passes through the origin (0,0). The function can take both positive and negative values.
Rational Functions: A Ratio of Polynomials
A rational function is a function that can be expressed as the quotient of two polynomials, f(x) = P(x) / Q(x), where P(x) and Q(x) are polynomials, and Q(x) is not the zero polynomial.
Key Features of Rational Functions
- Domain: The domain of a rational function is all real numbers except for the values of x that make the denominator Q(x) equal to zero. These values lead to vertical asymptotes.
- Vertical Asymptotes: These are vertical lines where the function approaches positive or negative infinity. They occur at the values of x where the denominator is zero and the numerator is non-zero.
- Horizontal Asymptotes: These are horizontal lines that the function approaches as x approaches positive or negative infinity. The existence and location of horizontal asymptotes depend on the degrees of the numerator and denominator polynomials.
- Oblique (Slant) Asymptotes: These occur when the degree of the numerator is exactly one greater than the degree of the denominator.
- x-intercepts: These are the points where the graph intersects the x-axis (where f(x) = 0). They occur when the numerator P(x) is zero and the denominator Q(x) is non-zero.
- y-intercepts: This is the point where the graph intersects the y-axis (where x = 0). It is found by evaluating f(0), provided that Q(0) is not zero.
Finding Asymptotes
Vertical Asymptotes: Set the denominator equal to zero and solve for x. These solutions (excluding those that also make the numerator zero) are the vertical asymptotes.
Horizontal Asymptotes:
- If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is y = 0.
- If the degree of the numerator is equal to the degree of the denominator, the horizontal asymptote is y = (leading coefficient of numerator) / (leading coefficient of denominator).
- If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote (there might be an oblique asymptote).
Oblique Asymptotes: Perform polynomial long division to divide the numerator by the denominator. The quotient (excluding the remainder) represents the oblique asymptote.
Graphing Rational Functions
Graphing rational functions involves identifying key features like intercepts, asymptotes, and the behavior of the function near these features. Plotting additional points can help refine the graph's shape.
Steps for Graphing Rational Functions
- Find the domain: Determine the values of x that make the denominator zero.
- Find the x-intercepts: Set the numerator equal to zero and solve for x.
- Find the y-intercept: Evaluate f(0) (if defined).
- Find the vertical asymptotes: Set the denominator equal to zero and solve for x.
- Find the horizontal or oblique asymptotes: Compare the degrees of the numerator and denominator polynomials.
- Analyze the behavior of the function near the asymptotes: Determine whether the function approaches positive or negative infinity on either side of each vertical asymptote.
- Plot additional points: Choose some x-values (especially between and beyond the vertical asymptotes) and evaluate the corresponding y-values.
- Sketch the graph: Draw a smooth curve that passes through the intercepts and approaches the asymptotes.
Solving Rational Equations and Inequalities
Rational equations and inequalities involve rational functions. Solving them often requires finding a common denominator, factoring, and considering the domain restrictions.
Techniques for Solving Rational Equations
- Find the common denominator: Multiply both sides of the equation by the common denominator to eliminate fractions.
- Solve the resulting polynomial equation: Use factoring, the quadratic formula, or other techniques to solve for x.
- Check for extraneous solutions: Verify that the solutions found do not make the original denominator zero. Any solutions that lead to division by zero are extraneous and must be discarded.
Techniques for Solving Rational Inequalities
- Find a common denominator: Rewrite the inequality with a common denominator.
- Determine critical values: These are the values of x that make the numerator or denominator zero.
- Test intervals: Test values from each interval created by the critical values to determine the sign of the expression in each interval.
- Write the solution: Express the solution as a union of intervals where the inequality holds true.
Applications of Polynomials and Rational Functions
Polynomials and rational functions have widespread applications in various fields:
- Physics: Modeling projectile motion, describing the relationship between distance, velocity, and acceleration.
- Engineering: Designing curves for roads and bridges, analyzing electrical circuits.
- Economics: Modeling supply and demand, analyzing cost functions.
- Computer Science: Developing algorithms, representing data structures.
- Statistics: Curve fitting, regression analysis.
This comprehensive guide provides a solid foundation in understanding polynomials and rational functions. Mastering these concepts is crucial for success in higher-level mathematics and numerous scientific and engineering disciplines. Remember to practice solving various problems to solidify your understanding and build confidence in tackling more complex scenarios. Through consistent practice and a deep understanding of the underlying principles, you'll be well-equipped to explore the fascinating world of polynomial and rational functions effectively.
Latest Posts
Latest Posts
-
How Do You Beat Stage 9 On Bloxorz
Jul 06, 2025
-
What Is 1 2 Equivalent To In Fractions
Jul 06, 2025
-
How Do You Say Pork In Spanish
Jul 06, 2025
Related Post
Thank you for visiting our website which covers about Unit 3 Power Polynomials And Rational Functions . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.