Volume Is The Amount Of An Object Occupies
Kalali
Apr 01, 2025 · 6 min read
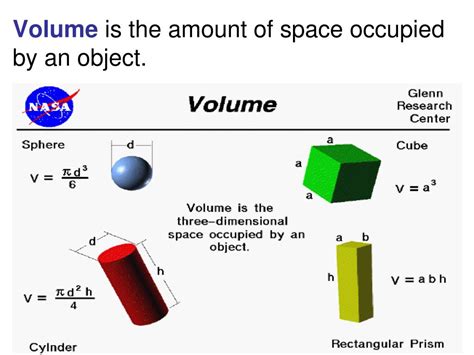
Table of Contents
Volume: Understanding the Space an Object Occupies
Volume, a fundamental concept in physics and mathematics, refers to the amount of three-dimensional space that an object or substance occupies. Understanding volume is crucial across various disciplines, from everyday tasks to complex scientific calculations. This comprehensive guide will explore the intricacies of volume, its measurement, calculation methods, and its applications in diverse fields.
What is Volume? A Deeper Dive
While the basic definition is straightforward – the space something takes up – a deeper understanding requires considering different aspects:
-
Three-Dimensional Space: Volume isn't a flat, two-dimensional measurement like area. It considers length, width, and height (or depth), encompassing the entire space within an object's boundaries. Imagine a cube: its volume represents the space enclosed within its six faces.
-
Units of Measurement: Volume is measured in cubic units, such as cubic centimeters (cm³), cubic meters (m³), cubic feet (ft³), cubic inches (in³), and liters (L). The choice of unit depends on the size of the object being measured. Microscopic objects might use cubic micrometers (µm³), while vast spaces like oceans utilize cubic kilometers (km³).
-
Regular vs. Irregular Shapes: Calculating the volume of regular shapes (cubes, spheres, cylinders) is relatively straightforward using established formulas. However, determining the volume of irregular shapes requires more sophisticated techniques, often involving displacement methods or numerical approximations.
-
Density and Volume: Volume is intrinsically linked to density. Density is defined as mass per unit volume (ρ = m/V). Knowing the volume and mass of an object allows us to calculate its density, a crucial property in materials science and engineering. High-density materials pack more mass into a given volume compared to low-density materials.
-
Volume and Capacity: The terms "volume" and "capacity" are often used interchangeably, but there's a subtle distinction. Volume refers to the space occupied by an object itself, while capacity refers to the amount of substance a container can hold. For instance, a bottle's volume is the space it occupies, while its capacity is the volume of liquid it can contain.
Calculating Volume: Formulas and Methods
The method for calculating volume depends heavily on the shape of the object. Let's explore some common shapes and their respective formulas:
Regular Shapes:
- Cube: Volume = side³ (where 'side' is the length of one side)
- Cuboid (Rectangular Prism): Volume = length × width × height
- Sphere: Volume = (4/3)πr³ (where 'r' is the radius)
- Cylinder: Volume = πr²h (where 'r' is the radius and 'h' is the height)
- Cone: Volume = (1/3)πr²h (where 'r' is the radius and 'h' is the height)
- Pyramid: Volume = (1/3)Bh (where 'B' is the area of the base and 'h' is the height)
Irregular Shapes:
Calculating the volume of irregular shapes presents a greater challenge. Several methods can be employed:
-
Water Displacement Method: This is a simple yet effective technique. Submerge the object in a container filled with water, measuring the volume of water displaced. The volume of the displaced water is equal to the volume of the object. This is widely used for irregularly shaped objects that are impervious to water.
-
Numerical Integration: For complex shapes, numerical integration techniques can provide accurate volume estimations. These methods divide the object into small, manageable elements, calculate the volume of each element, and then sum them up to approximate the total volume. This often utilizes computer software for complex geometries.
-
3D Scanning and Modeling: Advanced techniques like 3D scanning create a digital model of the object. Specialized software can then calculate the volume of this digital model with high precision. This is particularly useful in fields like medical imaging and industrial design where precise volume measurements are critical.
-
Cavalieri's Principle: This principle states that if two solids have the same height and the areas of their corresponding cross-sections are always equal, then the solids have the same volume. This can simplify volume calculations for certain irregular shapes by comparing them to simpler shapes with known volumes.
Units of Volume: A Global Perspective
The units used to measure volume vary depending on the context and geographical location. Here's a breakdown of common units:
-
Metric System (SI): The standard unit is the cubic meter (m³). Other common units include cubic centimeters (cm³), cubic millimeters (mm³), and liters (L) (1 L = 1000 cm³). The metric system's decimal-based nature simplifies conversions.
-
Imperial System: The imperial system uses cubic feet (ft³), cubic inches (in³), gallons (gal), and quarts (qt). Conversions within the imperial system can be more complex due to its inconsistent unit relationships.
-
Conversions: Accurate conversions between different units are essential for various applications. Online converters and conversion tables are readily available to facilitate this process.
Applications of Volume Measurement
The measurement and understanding of volume are crucial across a broad spectrum of fields:
Science and Engineering:
-
Fluid Mechanics: Volume is fundamental in understanding fluid flow, pressure, and buoyancy. Calculating the volume of reservoirs, pipelines, and containers is vital in designing and managing fluid systems.
-
Materials Science: Density, a ratio of mass to volume, is a key property of materials. Volume measurements are necessary for determining the density of substances, crucial for characterizing material properties and behavior.
-
Chemistry: Volume is essential in stoichiometry, which deals with quantitative relationships between reactants and products in chemical reactions. Titration, a common chemical technique, relies on precise volume measurements.
-
Physics: Volume plays a role in various areas, such as thermodynamics, where volume changes influence the properties of gases, and mechanics, where volume considerations are important in analyzing object displacement.
Medicine:
-
Medical Imaging: Techniques like MRI and CT scans provide three-dimensional images of the body, allowing for precise volume measurements of organs and tissues. This information is essential for diagnosis, treatment planning, and monitoring disease progression.
-
Drug Delivery: Accurate volume measurements are crucial in administering medications intravenously or orally. Incorrect dosages can have severe health consequences.
-
Blood Volume: Monitoring blood volume is vital in various medical situations. Precise volume measurements are essential for ensuring appropriate fluid balance and managing blood loss.
Everyday Life:
-
Cooking: Recipes often specify volumes of ingredients, such as cups or milliliters. Accurate volume measurements ensure consistent results in cooking and baking.
-
Construction: Calculating the volume of materials like concrete, sand, and gravel is necessary for estimating project costs and ensuring adequate supplies.
-
Packaging: Product packaging often specifies the volume of the contents. Accurate volume measurements are crucial for correct labeling and consumer information.
Advanced Concepts and Challenges
Beyond basic volume calculations, more advanced concepts and challenges exist:
-
Irregular Volumes and Fractals: Calculating the volume of highly irregular shapes or fractal objects poses significant challenges. Specialized mathematical techniques and computer simulations are often required.
-
Volume Changes with Temperature and Pressure: The volume of substances, especially gases and liquids, can vary with changes in temperature and pressure. Understanding these relationships is vital in various applications.
-
Volume of Complex Shapes in CAD Software: Computer-aided design (CAD) software provides advanced tools for calculating the volume of highly complex three-dimensional shapes. These tools are used extensively in engineering, manufacturing, and design.
Conclusion: Mastering the Concept of Volume
Understanding volume is a fundamental aspect of numerous scientific and practical endeavors. From basic calculations for simple shapes to sophisticated methods for complex objects, mastering volume measurement empowers accurate analysis, efficient design, and precise problem-solving across diverse fields. Whether you are a student, engineer, scientist, or simply curious about the world around you, a firm grasp of the concept of volume will enhance your understanding of the physical world and unlock a deeper appreciation of its quantitative nature. The continued development of advanced techniques and computational tools promises to further refine our ability to measure and understand volume in increasingly complex contexts.
Latest Posts
Latest Posts
-
What Is The Least Common Multiple For 9 And 12
Apr 02, 2025
-
What Is 45 C In F
Apr 02, 2025
-
How Many Feet In 180 Inches
Apr 02, 2025
-
450 Degree Celsius What In Fahrenheit
Apr 02, 2025
-
What Is 25 Percent Of 60
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Volume Is The Amount Of An Object Occupies . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
