What Are The Factors Of 37
Kalali
Apr 05, 2025 · 6 min read
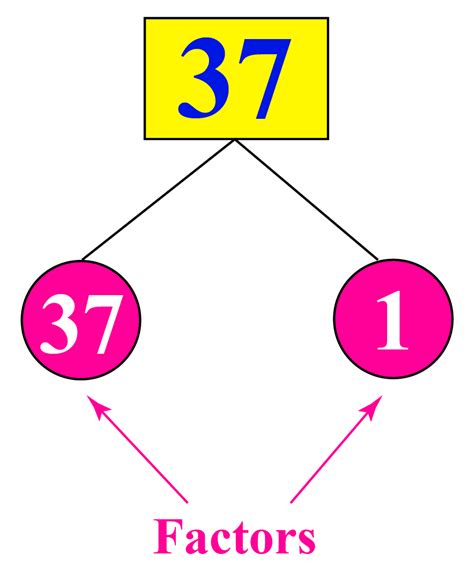
Table of Contents
What are the Factors of 37? A Deep Dive into Prime Numbers and Divisibility
The seemingly simple question, "What are the factors of 37?" opens a door to a fascinating world of number theory, prime numbers, and divisibility rules. While the immediate answer might seem straightforward, exploring this question allows us to delve into the fundamental concepts that underpin much of mathematics. This article will not only answer the question directly but will also explore the broader context of factors, prime numbers, and how to determine the factors of any number.
Understanding Factors and Divisibility
Before we tackle the factors of 37 specifically, let's define key terms. A factor (or divisor) of a number is a whole number that divides that number exactly without leaving a remainder. In simpler terms, it's a number that can be multiplied by another whole number to produce the original number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because:
- 1 x 12 = 12
- 2 x 6 = 12
- 3 x 4 = 12
Divisibility, on the other hand, refers to the property of a number being perfectly divisible by another number. If a number is divisible by another number, it means that the division results in a whole number quotient with no remainder.
Identifying the Factors of 37
Now, let's address the question at hand: What are the factors of 37? To find the factors of any number, we can systematically check all whole numbers from 1 up to the number itself. Let's do this for 37:
- 1: 1 x 37 = 37 (1 is a factor of every number)
- 37: 37 x 1 = 37 (The number itself is always a factor)
That's it! The only factors of 37 are 1 and 37.
The Significance of Prime Numbers
The fact that 37 has only two factors—1 and itself—makes it a prime number. A prime number is a whole number greater than 1 that has only two factors: 1 and itself. Prime numbers are the building blocks of all other whole numbers, as every whole number greater than 1 can be expressed as a unique product of prime numbers (this is known as the Fundamental Theorem of Arithmetic).
Prime numbers hold immense significance in mathematics and cryptography. Their unique properties make them essential in various areas, including:
- Cryptography: Prime numbers are crucial in developing secure encryption algorithms used to protect sensitive data online. The difficulty of factoring large numbers into their prime components forms the basis of many modern encryption methods.
- Number Theory: Prime numbers are central to many theorems and conjectures in number theory, a branch of mathematics that studies the properties of whole numbers. The study of prime numbers has led to significant advancements in our understanding of mathematical structures.
- Computer Science: Algorithms related to prime numbers are used in various computer science applications, such as primality testing and generating large prime numbers.
Methods for Finding Factors
While we manually found the factors of 37, there are several methods to find factors of larger numbers more efficiently. These include:
-
Trial Division: This method involves systematically testing each whole number from 1 up to the square root of the number. If a number divides the target number without a remainder, both that number and its quotient are factors. This method is effective for smaller numbers but can become computationally expensive for very large numbers.
-
Factorization Trees: This visual method helps break down a number into its prime factors. The process involves repeatedly dividing the number by its smallest prime factor until you reach 1. The prime factors are then identified from the branches of the tree.
-
Prime Factorization: This method aims to express a number as the product of its prime factors. For example, the prime factorization of 12 is 2 x 2 x 3 (or 2² x 3). This is the most fundamental way of representing a number's divisors.
Divisibility Rules
Understanding divisibility rules can help speed up the process of finding factors. Divisibility rules are shortcuts that allow you to determine whether a number is divisible by another number without performing the actual division. Here are a few examples:
- Divisibility by 2: A number is divisible by 2 if its last digit is even (0, 2, 4, 6, or 8).
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3.
- Divisibility by 5: A number is divisible by 5 if its last digit is 0 or 5.
- Divisibility by 10: A number is divisible by 10 if its last digit is 0.
While these rules don't directly find all factors, they help quickly eliminate numbers that are not factors.
Exploring Further: Beyond the Factors of 37
The seemingly simple question about the factors of 37 has led us on a journey through fundamental concepts in number theory. The fact that 37 is a prime number highlights the importance of these building blocks in mathematics and other fields. Understanding factors and divisibility is crucial not only for solving mathematical problems but also for appreciating the underlying structure of numbers. The exploration of prime numbers continues to be a vibrant area of research, with mathematicians constantly seeking to uncover new patterns and properties.
The methods for finding factors, along with divisibility rules, provide valuable tools for efficiently determining the factors of larger numbers. These techniques are not just theoretical exercises but have practical applications in various fields, particularly in cryptography and computer science. As we continue to explore the world of numbers, the seemingly simple question, "What are the factors of 37?", serves as a powerful reminder of the rich and complex beauty inherent in mathematics.
Advanced Concepts Related to Prime Numbers and Factorization
-
The Riemann Hypothesis: One of the most important unsolved problems in mathematics, the Riemann Hypothesis relates the distribution of prime numbers to the zeros of the Riemann zeta function.
-
The Twin Prime Conjecture: This conjecture proposes that there are infinitely many pairs of twin primes (primes that differ by 2, such as 3 and 5, or 11 and 13). While widely believed to be true, it remains unproven.
-
The Goldbach Conjecture: This conjecture states that every even integer greater than 2 can be expressed as the sum of two primes. This conjecture has been verified for extremely large numbers, but a general proof remains elusive.
These examples illustrate the ongoing quest to understand the intricate relationships within the realm of prime numbers. Further exploration into these and other advanced topics can significantly deepen your understanding of the mathematical world. The study of prime numbers remains a rich area of research, filled with challenges and breakthroughs.
The seemingly simple question of the factors of 37 has, therefore, opened a window to a vast and fascinating world of mathematical concepts and unsolved mysteries. From the basic definitions of factors and divisibility to the advanced concepts of prime number distribution and conjectures, the journey has been one of exploration and discovery. The exploration of numbers, particularly prime numbers, continues to be a fertile ground for mathematical research and innovation, with new insights and breakthroughs constantly emerging.
Latest Posts
Latest Posts
-
How Many Cups In 7 Oz
Apr 05, 2025
-
Cuanto Es 24 Oz En Litros
Apr 05, 2025
-
17 Is What Percent Of 20
Apr 05, 2025
-
What Is The Ratio For Sine
Apr 05, 2025
-
What Is 1 Percent Of 1000
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Are The Factors Of 37 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
