What Are The Two Square Roots Of 64
Kalali
Aug 20, 2025 · 7 min read
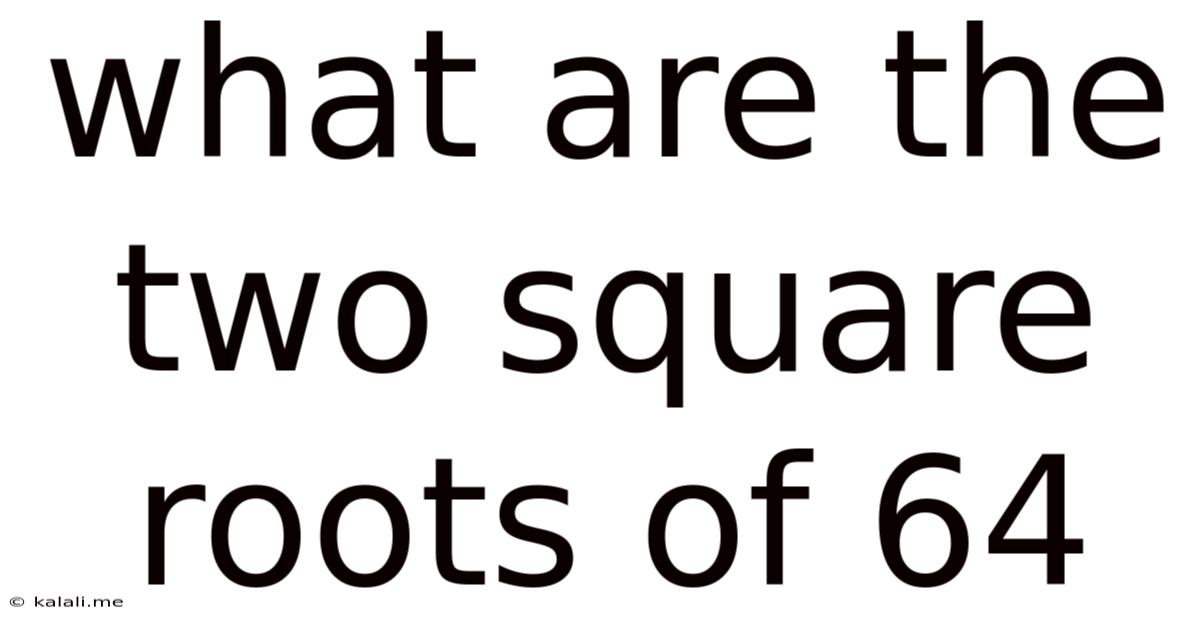
Table of Contents
What are the Two Square Roots of 64? Unpacking the Concept of Square Roots and Their Applications
What are the two square roots of 64? The simple answer is 8 and -8. However, understanding why this is the case delves into the fundamental concept of square roots, their mathematical properties, and their applications across various fields. This article will explore these aspects in detail, moving beyond the simple answer to provide a comprehensive understanding of square roots and their significance.
This article will cover:
- Understanding Square Roots: Defining the concept and its relationship to squares.
- The Two Square Roots: Explaining why every positive number has two square roots.
- Square Roots in Different Number Systems: Exploring square roots in real numbers, complex numbers, and beyond.
- Practical Applications of Square Roots: Showcasing the relevance of square roots in various fields like physics, engineering, and finance.
- Solving Equations Involving Square Roots: Illustrating how to solve equations containing square roots.
- Approximating Square Roots: Methods for finding approximate values of square roots when exact values are difficult to obtain.
- Square Roots and Geometry: Connecting the concept of square roots to geometric concepts like the Pythagorean theorem.
- Advanced Concepts: Briefly touching upon more complex concepts related to square roots, like nth roots and radical expressions.
Understanding Square Roots: The Inverse Operation of Squaring
A square root of a number is a value that, when multiplied by itself (squared), gives the original number. In simpler terms, it's the inverse operation of squaring. For example, the square of 3 (3²) is 9, therefore, the square root of 9 (√9) is 3. This is often expressed as: √9 = 3.
This understanding forms the basis for grasping the concept of two square roots. While we often focus on the principal square root (the positive one), it's crucial to remember that squaring a negative number also results in a positive number. For instance, (-3)² = 9. Therefore, -3 is also a square root of 9. This principle directly applies to the question: What are the two square roots of 64?
The Two Square Roots: Why 8 and -8?
The number 64 is a perfect square, meaning it's the square of an integer. We know that 8 multiplied by itself (8²) equals 64. However, (-8) multiplied by itself ((-8)²) also equals 64. This is because the product of two negative numbers is always positive. Therefore, both 8 and -8 are square roots of 64.
This concept is mathematically represented as:
- √64 = 8 (principal square root)
- -√64 = -8
The principal square root (√64 = 8) is the non-negative square root, the one usually presented as the answer when asking for "the" square root. However, it's essential to remember that there are always two square roots for any positive number, one positive and one negative.
Square Roots in Different Number Systems
The concept of square roots extends beyond the realm of integers. Let's examine their presence in other number systems:
-
Real Numbers: For every non-negative real number, there are two real square roots – a positive and a negative one. For negative real numbers, the square roots are complex numbers (discussed below).
-
Complex Numbers: Complex numbers extend the concept of real numbers to include imaginary units (represented as 'i', where i² = -1). The square root of a negative number, like √-9, can be expressed as a complex number: 3i and -3i. Every complex number (except 0) has two square roots.
-
Other Number Systems: The idea of square roots extends to more abstract mathematical structures, but the fundamental principle remains consistent: finding a number that, when multiplied by itself, results in the original number.
Practical Applications of Square Roots: Beyond the Textbook
Square roots are far from just an abstract mathematical concept. They have numerous practical applications in diverse fields:
-
Physics: Calculating speed, distance, and acceleration frequently involves square roots. The Pythagorean theorem, for example, uses square roots to determine the length of the hypotenuse of a right-angled triangle. This has implications in many areas of physics, from calculating the velocity of projectiles to determining the distance between points in space. The formula for calculating the kinetic energy of an object also involves a square root.
-
Engineering: Engineers use square roots extensively in structural calculations, determining stress and strain in materials, and calculating the forces acting on structures. Civil engineers utilize square roots when designing bridges and buildings; they employ the Pythagorean Theorem to calculate precise measurements and ensure stability. Electrical engineers also use square roots in calculating impedance and current in electrical circuits.
-
Finance: Standard deviation, a crucial concept in finance for measuring investment risk, utilizes square roots. Calculating the volatility of an asset also uses the standard deviation, which, in turn, relies on the square root function. Square roots are also important in financial modeling and risk assessment.
-
Computer Graphics: Square roots are crucial in 3D graphics rendering and transformations. Many of the underlying algorithms rely on the calculation of distances and vectors, which invariably uses square roots.
Solving Equations Involving Square Roots
Solving equations that involve square roots often requires careful consideration. Here's a simple example:
x² = 25
To solve for x, we take the square root of both sides:
√x² = ±√25
x = ±5
Note the ± sign, indicating that both 5 and -5 are solutions. When solving equations with square roots, always remember to consider both positive and negative solutions, unless the context indicates otherwise (e.g., a problem involving length or distance where negative values are unrealistic). Solving more complex equations might involve isolating the square root term, squaring both sides to eliminate the radical, and then solving the resulting equation. It's important to check your solutions to ensure they are valid and don't introduce extraneous solutions (solutions that don't satisfy the original equation).
Approximating Square Roots: Methods for Estimation
Not all numbers have easily calculable square roots. For instance, the square root of 2 (√2) is an irrational number, meaning it cannot be expressed as a simple fraction. In these cases, we can approximate the square root using various methods:
-
Babylonian Method (or Heron's Method): This iterative method refines an initial guess to progressively get closer to the actual square root. The formula is: x_(n+1) = (x_n + S/x_n) / 2, where x_n is the current guess and S is the number whose square root we are seeking.
-
Linear Approximation: This method uses the tangent line to the square root function at a known point to estimate the square root of a nearby number.
-
Using a Calculator: Modern calculators readily provide approximate values for square roots.
Square Roots and Geometry: The Pythagorean Theorem
The Pythagorean Theorem, a cornerstone of geometry, directly utilizes square roots. It states that in a right-angled triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides (the legs). The formula is: a² + b² = c², where 'a' and 'b' are the lengths of the legs, and 'c' is the length of the hypotenuse. To find the length of the hypotenuse, we need to take the square root of the sum of the squares of the legs: c = √(a² + b²). This theorem has wide-ranging applications in surveying, construction, and various aspects of engineering and physics.
Advanced Concepts: nth Roots and Radical Expressions
The concept of square roots expands to nth roots. An nth root of a number is a value that, when raised to the power of n, gives the original number. The square root is a specific case of an nth root where n=2. More complex expressions involving square roots and other radicals are often encountered in advanced mathematics. Understanding how to simplify and manipulate radical expressions is crucial in algebra and calculus.
In conclusion, while the answer to "What are the two square roots of 64?" is simply 8 and -8, the underlying concept of square roots encompasses much more. This exploration has shown that square roots are a fundamental mathematical concept with far-reaching applications across various disciplines. Understanding their properties, methods of calculation, and practical uses is essential for anyone pursuing studies or working in fields involving mathematics, science, or engineering. Remember, always consider both the positive and negative square roots unless the context explicitly restricts the solution.
Latest Posts
Latest Posts
-
How Do You Say Glue In Spanish
Aug 21, 2025
-
3 Bottles Of Water Is How Many Liters
Aug 21, 2025
-
Which Sport Does Not Require Core Muscle Strength
Aug 21, 2025
-
How Many Sq Ft In 1 3 Acre
Aug 21, 2025
-
How Many Ounces Of Garlic In A Clove
Aug 21, 2025
Related Post
Thank you for visiting our website which covers about What Are The Two Square Roots Of 64 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.