What Divided By 9 - 4 Equals 8
Kalali
Jul 06, 2025 · 4 min read
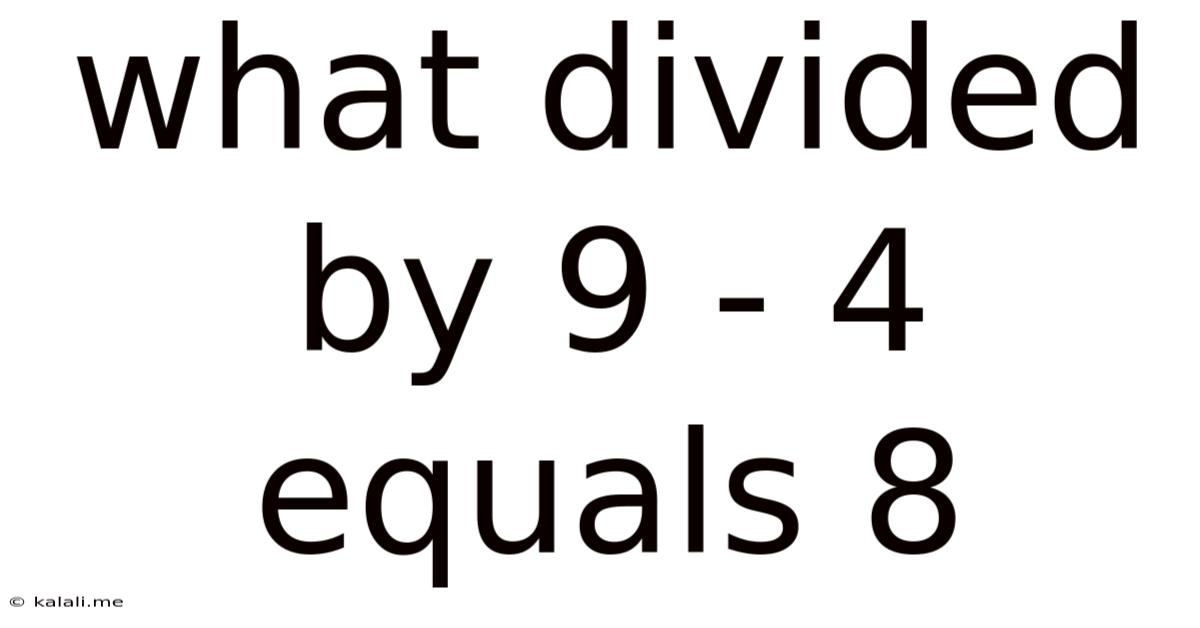
Table of Contents
What Divided by 9 Minus 4 Equals 8? Solving the Mathematical Puzzle
This article unravels the solution to the intriguing mathematical puzzle: "What divided by 9, minus 4, equals 8?" We'll not only find the answer but also explore the step-by-step process of solving this type of algebraic equation, providing a deeper understanding of the underlying mathematical principles. This approach is perfect for anyone looking to improve their problem-solving skills or brush up on their algebra. We’ll also explore related problems and how to approach them systematically.
Understanding the Problem:
The core of this problem lies in translating the word problem into a mathematical equation. The phrase "What divided by 9" suggests an unknown value, which we'll represent with the variable 'x'. The equation then becomes:
(x / 9) - 4 = 8
Our goal is to isolate 'x' and determine its value. This involves employing several algebraic manipulation techniques.
Solving the Equation Step-by-Step:
Here's a detailed breakdown of how to solve the equation (x / 9) - 4 = 8:
-
Add 4 to both sides: The first step is to eliminate the '-4' from the left side of the equation. To do this, we add 4 to both sides to maintain balance:
(x / 9) - 4 + 4 = 8 + 4
This simplifies to:
x / 9 = 12
-
Multiply both sides by 9: Now we need to isolate 'x' completely. Since 'x' is divided by 9, we multiply both sides of the equation by 9:
(x / 9) * 9 = 12 * 9
This results in:
x = 108
Therefore, the answer is 108. 108 divided by 9 is 12, and 12 minus 4 equals 8.
Verification:
It's always a good practice to verify the solution. Let's substitute x = 108 back into the original equation:
(108 / 9) - 4 = 8
12 - 4 = 8
8 = 8
The equation holds true, confirming that our solution, x = 108, is correct.
Expanding on Algebraic Manipulation Techniques:
Solving this type of equation relies on fundamental algebraic principles. Understanding these principles is crucial for tackling more complex mathematical problems. Here are some key techniques:
-
Order of Operations (PEMDAS/BODMAS): Remember the order of operations: Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right). Following this order ensures accurate calculations.
-
Inverse Operations: This involves using the opposite operation to undo an action. For example, addition and subtraction are inverse operations, as are multiplication and division. We used this principle when we added 4 to both sides to counteract the subtraction and multiplied by 9 to counteract the division.
-
Maintaining Equation Balance: The most crucial aspect of solving equations is maintaining balance. Whatever operation you perform on one side of the equation, you must perform the same operation on the other side to keep the equation equal.
Similar Problems and How to Approach Them:
Let's explore similar problems to enhance your understanding and problem-solving skills:
Problem 1: What number divided by 5, plus 3, equals 11?
- Translate to an equation: x / 5 + 3 = 11
- Subtract 3 from both sides: x / 5 = 8
- Multiply both sides by 5: x = 40
- Verify: (40 / 5) + 3 = 11 (8 + 3 = 11) Correct!
Problem 2: What number multiplied by 2, minus 7, equals 9?
- Translate to an equation: 2x - 7 = 9
- Add 7 to both sides: 2x = 16
- Divide both sides by 2: x = 8
- Verify: (2 * 8) - 7 = 9 (16 - 7 = 9) Correct!
Problem 3: (x/3) + 5 -2 = 10
- Simplify: (x/3) + 3 = 10
- Subtract 3 from both sides: x/3 = 7
- Multiply both sides by 3: x = 21
- Verify: (21/3) + 5 - 2 = 10 (7 + 5 - 2 = 10) Correct!
Advanced Problem Solving Techniques:
For more complex equations involving multiple variables or parentheses, consider these techniques:
-
Distributive Property: This property allows you to simplify expressions by multiplying a term outside parentheses with each term inside the parentheses: a(b + c) = ab + ac
-
Factoring: Factoring involves expressing an expression as a product of simpler expressions. This is often helpful when solving quadratic equations.
-
Quadratic Formula: For quadratic equations (equations of the form ax² + bx + c = 0), the quadratic formula provides a direct way to find the solutions for x.
Conclusion:
Solving the equation "What divided by 9 minus 4 equals 8" provides a valuable opportunity to practice fundamental algebraic principles. By understanding the step-by-step process, inverse operations, and maintaining equation balance, you can effectively solve a wide range of similar problems. Remember to always verify your solution by substituting the value back into the original equation. Practice consistently with various problem types, gradually increasing the complexity to build your mathematical skills and confidence. The ability to confidently solve algebraic equations is a valuable asset in many areas, from further mathematical studies to everyday problem-solving. This methodical approach can be applied to numerous real-world scenarios, making algebraic fluency a highly transferable skill.
Latest Posts
Latest Posts
-
How Long Are Hellofresh Meals Good For
Jul 07, 2025
-
How To Beat Wheely 6 Level 4
Jul 07, 2025
-
How Many Decimeters Are In A Meter
Jul 07, 2025
-
How Fast Is 500 Km Per Hour
Jul 07, 2025
-
How Do You Say Butt In Spanish
Jul 07, 2025
Related Post
Thank you for visiting our website which covers about What Divided By 9 - 4 Equals 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.