What Dvied By 3 Gives U 7
Kalali
Aug 20, 2025 · 5 min read
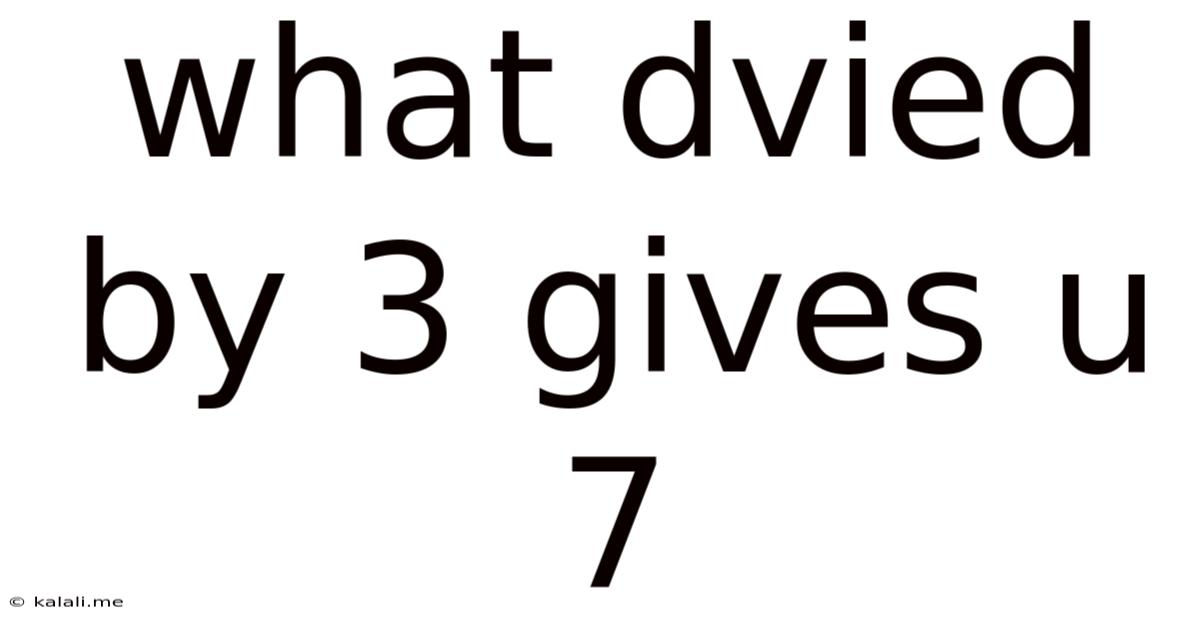
Table of Contents
What Divided by 3 Gives You 7? Unraveling the Mystery of Simple Division
This seemingly simple question, "What divided by 3 gives you 7?", is a great entry point into understanding fundamental mathematical concepts. While the answer itself is straightforward, exploring the methods to solve it and expanding on the underlying principles reveals a deeper appreciation for arithmetic and its applications. This article will not only provide the solution but also delve into various approaches, illustrating the beauty and logic inherent in mathematical problem-solving. We'll explore different techniques, discuss their advantages and disadvantages, and even touch upon how this simple problem can be extended to more complex scenarios.
Understanding the Problem: A Mathematical Equation
The question, "What divided by 3 gives you 7?", can be elegantly expressed as a simple algebraic equation: x / 3 = 7. Here, 'x' represents the unknown number we're trying to find. The equation signifies that when we divide 'x' by 3, the result is 7. Our task is to solve for 'x'.
Method 1: The Inverse Operation – Multiplication
The most direct method to solve for 'x' is to employ the inverse operation of division: multiplication. Since division by 3 is the operation performed on 'x', we can undo this by multiplying both sides of the equation by 3.
- Starting Equation: x / 3 = 7
- Multiply both sides by 3: (x / 3) * 3 = 7 * 3
- Simplify: x = 21
Therefore, the number that, when divided by 3, gives you 7 is 21. This method is intuitive and efficient, making it a preferred approach for solving simple algebraic equations.
Method 2: Working Backwards – A Logical Approach
Another way to approach this problem is by working backwards from the given information. We know that the result of dividing an unknown number by 3 is 7. Thinking logically, if we reverse the process, we can find the original number. This involves multiplying the result (7) by the divisor (3).
- Result: 7
- Divisor: 3
- Calculation: 7 * 3 = 21
Again, we arrive at the solution: 21. This method highlights the interconnectedness of arithmetic operations and how reversing them can be a powerful tool for problem-solving.
Method 3: Visual Representation – Using Models
While less efficient for simple equations, visualizing the problem can be beneficial for understanding the concept, especially when teaching children. Imagine dividing a group of objects into three equal parts. If each part contains 7 objects, the total number of objects is 7 * 3 = 21. This visual approach helps solidify the understanding of division and its relationship to multiplication.
Expanding the Concept: Generalizing the Solution
The problem "What divided by 3 gives you 7?" is a specific instance of a broader class of problems. We can generalize this to: "What divided by 'a' gives you 'b'?" This can be expressed algebraically as: x / a = b. The solution, using the inverse operation, is always: x = a * b. This generalized solution allows us to solve similar problems with different values for 'a' and 'b'.
Applications in Real-World Scenarios
This seemingly simple mathematical problem has numerous real-world applications:
- Sharing Equally: Imagine sharing 21 candies among 3 friends equally. Each friend would receive 21 / 3 = 7 candies.
- Resource Allocation: If you need to allocate 21 workers across 3 teams equally, each team would receive 21 / 3 = 7 workers.
- Unit Conversion: Consider converting 21 meters into groups of 3 meters each. You would have 21 / 3 = 7 groups.
- Recipe Scaling: If a recipe calls for 7 cups of flour per serving and you want to make 3 servings, you would need 7 * 3 = 21 cups of flour.
Beyond Basic Arithmetic: Connecting to Advanced Concepts
Understanding this simple division problem lays the groundwork for more complex mathematical concepts:
- Algebra: Solving algebraic equations is fundamental to higher-level mathematics. This problem demonstrates the basic principles of solving for an unknown variable.
- Calculus: Calculus relies heavily on the understanding of limits and rates of change, both of which build upon fundamental arithmetic operations.
- Programming: Solving equations like this is a crucial aspect of programming, where algorithms often require solving for unknown variables.
- Data Analysis: Many statistical analyses involve manipulating data using arithmetic operations, making a solid understanding of basic arithmetic essential.
Error Analysis and Common Mistakes
While the solution is straightforward, common errors can occur, particularly for beginners:
- Incorrect Order of Operations: Confusing the order of operations can lead to incorrect results. Remember to perform division before multiplication (unless parentheses dictate otherwise).
- Misunderstanding Division: A lack of understanding of the concept of division itself can lead to errors. Understanding the relationship between division and multiplication is crucial.
- Computational Errors: Simple calculation errors can also occur. Double-checking your work is always recommended.
Conclusion: The Power of Simple Problems
The seemingly trivial question, "What divided by 3 gives you 7?", reveals a wealth of mathematical principles and real-world applications. By exploring various methods for solving this simple problem, we’ve highlighted the importance of understanding fundamental arithmetic operations, the power of inverse operations, and the ability to generalize solutions to tackle more complex problems. The journey from a simple equation to a broader understanding of mathematical concepts underscores the importance of appreciating even the most basic mathematical exercises. This problem showcases how a seemingly simple question can serve as a springboard for learning and understanding much broader mathematical concepts, emphasizing the power of foundational knowledge in all aspects of mathematical problem-solving and application. From basic arithmetic to advanced calculus, the principles illustrated here are fundamental and enduring.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 8 And 4
Aug 21, 2025
-
How Do You Say Glue In Spanish
Aug 21, 2025
-
3 Bottles Of Water Is How Many Liters
Aug 21, 2025
-
Which Sport Does Not Require Core Muscle Strength
Aug 21, 2025
-
How Many Sq Ft In 1 3 Acre
Aug 21, 2025
Related Post
Thank you for visiting our website which covers about What Dvied By 3 Gives U 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.