What Fraction Is Equal To 3 5
Kalali
Aug 22, 2025 · 5 min read
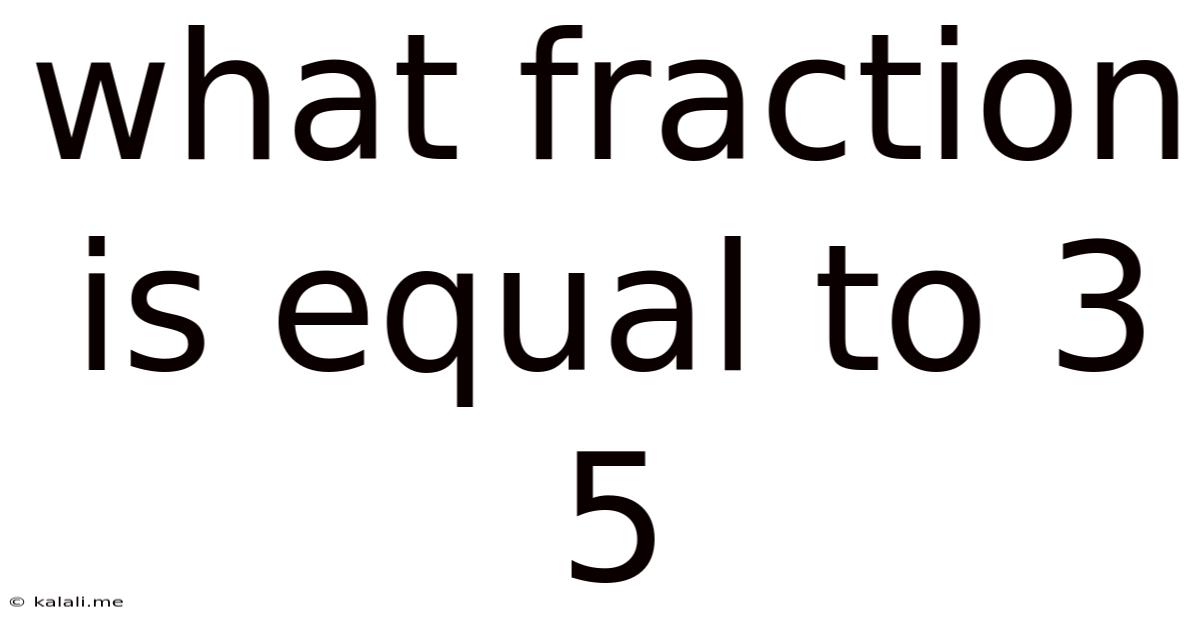
Table of Contents
Decoding the Fraction: What Fraction is Equal to 3/5? A Deep Dive into Fractions and Equivalent Fractions
This seemingly simple question, "What fraction is equal to 3/5?", opens a door to a fascinating world of mathematical concepts. While the answer might seem immediately obvious, understanding the underlying principles of fractions and equivalent fractions is crucial for mastering arithmetic and algebra. This article will delve deep into the concept, exploring not only the answer but also the broader implications and applications of equivalent fractions. We'll unravel the mysteries of fraction simplification, explore different ways to represent the same fractional value, and touch upon the practical applications of this fundamental mathematical idea.
Meta Description: This article comprehensively explores the question "What fraction is equal to 3/5?", explaining equivalent fractions, simplification, and real-world applications. Learn how to identify and work with fractions representing the same value.
Understanding Fractions: A Quick Refresher
Before we dive into the specifics of 3/5, let's establish a firm understanding of what a fraction represents. A fraction is a numerical representation of a part of a whole. It's expressed as a ratio of two integers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into.
For example, in the fraction 3/5, the numerator (3) represents 3 parts, and the denominator (5) signifies that the whole has been divided into 5 equal parts. This means we have 3 out of 5 equal parts of the whole.
What Fraction is Equal to 3/5? The Simple Answer
The simplest answer to the question "What fraction is equal to 3/5?" is... 3/5. There is no simpler, irreducible fraction equivalent to 3/5. However, the question prompts a broader understanding of equivalent fractions. While 3/5 is the simplest form, infinitely many other fractions represent the same value.
The Concept of Equivalent Fractions
Equivalent fractions represent the same portion of a whole, even though they appear different. This is achieved by multiplying or dividing both the numerator and denominator by the same non-zero number. This process maintains the ratio between the numerator and the denominator, thus preserving the fractional value.
Think of it like slicing a pizza: If you have a pizza cut into 5 slices and you eat 3, you've eaten 3/5 of the pizza. Now imagine someone else has the same size pizza, but it's cut into 10 slices. If they eat 6 slices, they've also eaten 3/5 of their pizza (6/10). Both 3/5 and 6/10 represent the same portion of the pizza.
Finding Equivalent Fractions for 3/5
To find equivalent fractions for 3/5, we can multiply both the numerator and denominator by the same number:
- Multiply by 2: (3 x 2) / (5 x 2) = 6/10
- Multiply by 3: (3 x 3) / (5 x 3) = 9/15
- Multiply by 4: (3 x 4) / (5 x 4) = 12/20
- Multiply by 5: (3 x 5) / (5 x 5) = 15/25
- And so on…
We can continue this process indefinitely, generating an infinite number of equivalent fractions for 3/5. Each of these fractions represents the same proportion or value as 3/5.
Simplifying Fractions: Finding the Simplest Form
Conversely, we can simplify fractions by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
For example, let's take the equivalent fraction 15/25. The GCD of 15 and 25 is 5. Dividing both the numerator and denominator by 5 gives us:
15 ÷ 5 / 25 ÷ 5 = 3/5
This demonstrates that 15/25 simplifies to 3/5, confirming that they are equivalent fractions. 3/5 is the simplest form because the numerator and denominator share no common factors other than 1.
Visualizing Equivalent Fractions
Visual aids can greatly enhance understanding. Imagine a rectangle divided into 5 equal parts. Shading 3 of those parts represents 3/5. Now, imagine dividing each of those 5 parts into 2 more equal parts. You now have 10 parts in total, and 6 of them are shaded. This visually confirms that 3/5 and 6/10 are equivalent.
Practical Applications of Equivalent Fractions
Understanding equivalent fractions is not just an abstract mathematical concept; it's crucial in numerous real-world scenarios:
-
Cooking and Baking: Recipes often require adjusting ingredient quantities. If a recipe calls for 3/5 of a cup of flour, and you want to double the recipe, you need to find an equivalent fraction for 6/10 or 1 1/5 cups.
-
Measurement and Conversions: Converting between different units of measurement (e.g., inches to feet, centimeters to meters) often involves working with equivalent fractions.
-
Financial Calculations: Dealing with percentages, proportions, and ratios in finance heavily relies on the understanding and manipulation of equivalent fractions.
-
Data Analysis and Statistics: Equivalent fractions play a vital role in data representation and interpretation, ensuring consistent and accurate analysis.
Beyond 3/5: Extending the Concept
The principles discussed here apply to any fraction. You can find equivalent fractions for any given fraction by multiplying or dividing both the numerator and denominator by the same non-zero number. Similarly, you can simplify any fraction by finding the greatest common divisor of the numerator and the denominator and dividing both by it.
This understanding is a cornerstone for further mathematical explorations, including working with mixed numbers, improper fractions, and performing more complex arithmetic operations with fractions.
Conclusion: Mastering the Art of Fractions
The question "What fraction is equal to 3/5?" serves as a springboard for a deeper understanding of fractions, equivalent fractions, and their practical applications. While the simplest answer is 3/5, the journey to understanding the concept reveals a wealth of mathematical principles vital for success in various fields. By mastering the manipulation and interpretation of equivalent fractions, we unlock a powerful tool for problem-solving and a deeper appreciation for the elegance of mathematics. This fundamental understanding lays the groundwork for more advanced mathematical concepts and their real-world applications. From baking a cake to analyzing financial data, the ability to work confidently with fractions is an invaluable skill.
Latest Posts
Latest Posts
-
How Do You Say Your Handsome In Spanish
Aug 22, 2025
-
How To Make A Snow Globe Without Glycerin
Aug 22, 2025
-
What Year Are 22 Year Olds Born
Aug 22, 2025
-
Which Of The Following Statements Regarding Mrs Morningstar Is Wrong
Aug 22, 2025
-
What Number Has The Letter J In It
Aug 22, 2025
Related Post
Thank you for visiting our website which covers about What Fraction Is Equal To 3 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.