What Fraction Is Equal To 5 6
Kalali
Jul 21, 2025 · 5 min read
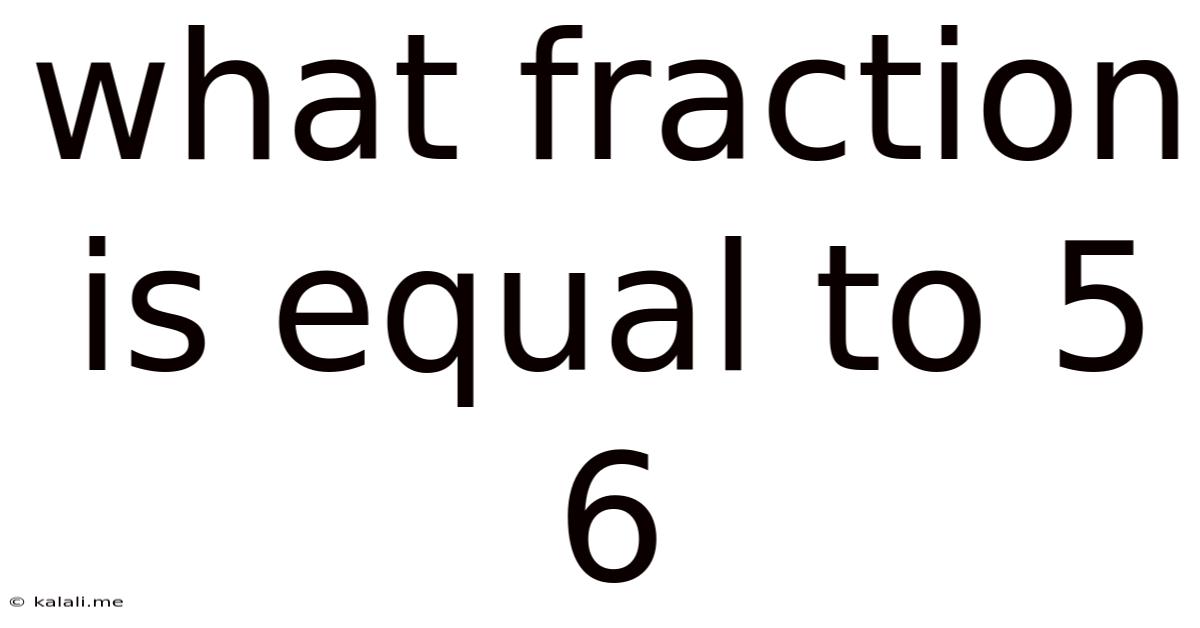
Table of Contents
What Fraction is Equal to 5/6? Understanding Fractions and Equivalent Fractions
This seemingly simple question, "What fraction is equal to 5/6?", opens the door to a deeper understanding of fractions, their properties, and how to manipulate them. While the answer might seem obvious at first glance – 5/6 is equal to 5/6 – the real value lies in exploring the concept of equivalent fractions and how to find them. This article will delve into the intricacies of fractions, providing a comprehensive explanation for both beginners and those looking to solidify their understanding.
Meta Description: Discover the world of fractions! Learn what fractions are equivalent to 5/6, how to find equivalent fractions, and master the fundamental concepts of fraction simplification and representation. This comprehensive guide covers everything you need to know about fractions.
Understanding Fractions: A Foundation
Before diving into equivalent fractions, let's revisit the fundamental concepts of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into.
For example, in the fraction 5/6, 5 is the numerator, and 6 is the denominator. This means we have 5 parts out of a possible 6 equal parts.
Finding Equivalent Fractions: The Key to Understanding 5/6
The core of this discussion lies in understanding equivalent fractions. Equivalent fractions represent the same proportion or value, even though they look different. They are essentially different ways of expressing the same part of a whole. To find equivalent fractions, you simply multiply or divide both the numerator and the denominator by the same non-zero number. This process doesn't change the overall value of the fraction.
Let's illustrate this with 5/6. We can find equivalent fractions by multiplying both the numerator and the denominator by the same number:
- Multiply by 2: (5 x 2) / (6 x 2) = 10/12
- Multiply by 3: (5 x 3) / (6 x 3) = 15/18
- Multiply by 4: (5 x 4) / (6 x 4) = 20/24
- Multiply by 5: (5 x 5) / (6 x 5) = 25/30
- And so on...
All of these fractions – 10/12, 15/18, 20/24, 25/30, etc. – are equivalent to 5/6. They represent the same portion of a whole.
Conversely, we can also find equivalent fractions by dividing both the numerator and the denominator by a common factor. However, in the case of 5/6, this isn't possible because 5 and 6 don't share any common factors other than 1. This means that 5/6 is already in its simplest form.
Visualizing Equivalent Fractions
Visual aids can significantly enhance understanding. Imagine a pizza cut into 6 slices. The fraction 5/6 represents having 5 out of those 6 slices. Now, imagine cutting each of those 6 slices in half. You now have 12 slices, and you still have 10 of them (5 x 2). This represents the equivalent fraction 10/12. The proportion remains the same; you still have the same amount of pizza.
This visual representation helps to concretely demonstrate that equivalent fractions represent the same quantity, regardless of the numbers used to express them.
Simplifying Fractions: Reducing to Lowest Terms
While we can generate infinitely many equivalent fractions by multiplying the numerator and denominator, it's often beneficial to simplify fractions to their lowest terms. This means reducing the fraction to its simplest form, where the numerator and denominator have no common factors other than 1.
As mentioned earlier, 5/6 is already in its simplest form because 5 and 6 share no common factors greater than 1 (they are relatively prime).
Applications of Equivalent Fractions in Real Life
Understanding equivalent fractions isn't just an academic exercise; it has practical applications in various aspects of daily life:
- Cooking and Baking: Recipes often require adjusting ingredient quantities. Equivalent fractions allow for accurate scaling of recipes up or down.
- Measurements: Converting between different units of measurement, such as inches and feet, involves using equivalent fractions.
- Construction and Engineering: Accurate calculations in construction and engineering rely heavily on precise fraction manipulation and understanding equivalent fractions to ensure structural integrity and functionality.
- Finance: Understanding proportions and ratios, essential in finance, uses the principles of equivalent fractions.
Beyond 5/6: Exploring Other Fractions and Their Equivalents
The principles discussed here apply to all fractions. Let's explore some examples:
- 1/2: Equivalent fractions include 2/4, 3/6, 4/8, and so on.
- 2/3: Equivalent fractions include 4/6, 6/9, 8/12, and so on.
- 3/4: Equivalent fractions include 6/8, 9/12, 12/16, and so on.
By applying the principle of multiplying or dividing both the numerator and denominator by the same number, you can find countless equivalent fractions for any given fraction.
Improper Fractions and Mixed Numbers: Expanding the Understanding
So far, we've focused on proper fractions (where the numerator is smaller than the denominator). However, there are also improper fractions (where the numerator is greater than or equal to the denominator) and mixed numbers (a combination of a whole number and a proper fraction).
Let's consider an improper fraction like 7/3. This is equivalent to 2 1/3 (two and one-third). This illustrates the relationship between improper fractions and mixed numbers. Converting between them is another essential skill in fraction manipulation.
Mastering Fractions: A Continuous Journey
Understanding fractions, including finding equivalent fractions for a given fraction like 5/6, is a fundamental skill in mathematics. It's a building block for more complex mathematical concepts. The more you practice working with fractions, the more intuitive and comfortable you'll become. Regular practice, coupled with visual aids and real-world applications, will help solidify your understanding and enable you to confidently tackle any fraction-related problem.
Conclusion: The Significance of 5/6 and Equivalent Fractions
Returning to the initial question, "What fraction is equal to 5/6?", the answer is not just 5/6 itself but also an infinite set of equivalent fractions. Understanding this concept, along with the ability to simplify fractions and convert between different forms, is crucial for success in mathematics and various real-world applications. Mastering fractions is a journey of understanding proportions, ratios, and the representation of parts of a whole. The seemingly simple fraction 5/6 serves as a gateway to a deeper appreciation of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
What Did The Policeman Tell The Burglar In The Bathroom
Jul 21, 2025
-
Firing Order For A 2000 Ford Ranger 3 0
Jul 21, 2025
-
Why Did Brady Leave Pair Of Kings
Jul 21, 2025
-
100 Km An Hour To Miles Per Hour
Jul 21, 2025
-
How Many Ounces In A Quarter Teaspoon
Jul 21, 2025
Related Post
Thank you for visiting our website which covers about What Fraction Is Equal To 5 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.