What Fraction Is Equal To 6 8
Kalali
Jul 21, 2025 · 5 min read
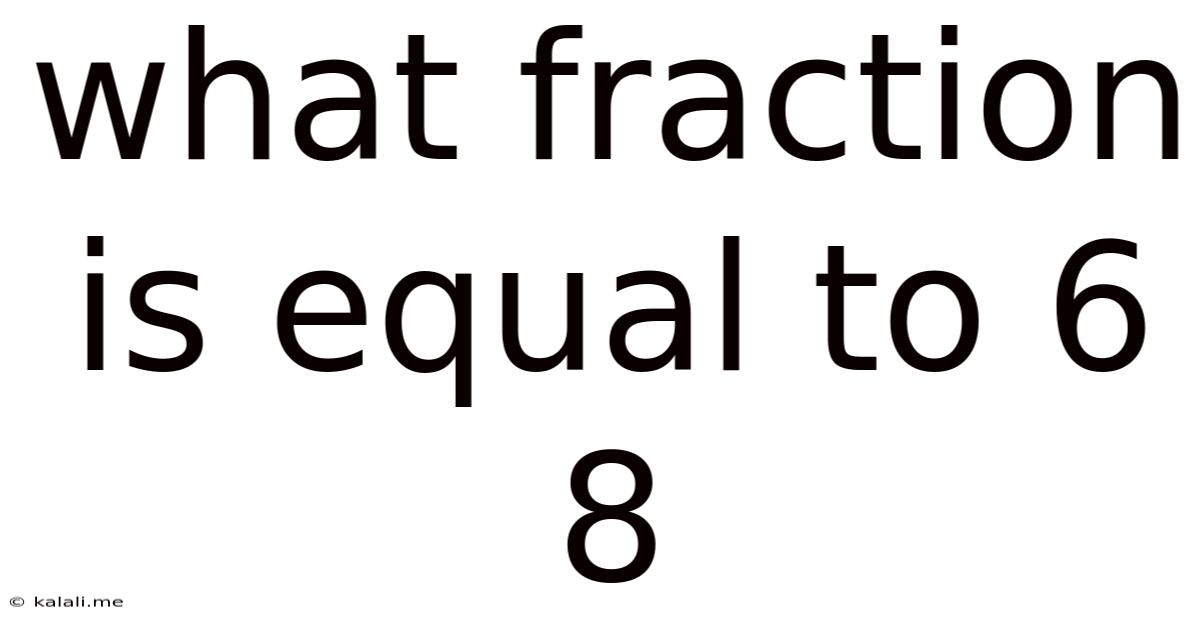
Table of Contents
What Fraction is Equal to 6/8? Simplifying Fractions and Understanding Equivalence
This seemingly simple question, "What fraction is equal to 6/8?", opens a door to a fundamental concept in mathematics: fraction equivalence. Understanding how to simplify fractions and identify equivalent fractions is crucial for various mathematical operations and applications. This article will delve into the intricacies of simplifying 6/8, exploring the underlying principles and providing a comprehensive understanding of equivalent fractions. We'll go beyond the simple answer and explore the broader implications of this seemingly basic concept.
Understanding Fractions: Numerator and Denominator
Before we tackle the simplification of 6/8, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two key components:
- Numerator: The top number represents the number of parts we have. In the fraction 6/8, the numerator is 6.
- Denominator: The bottom number represents the total number of equal parts the whole is divided into. In the fraction 6/8, the denominator is 8.
Therefore, 6/8 means we have 6 parts out of a total of 8 equal parts.
Simplifying Fractions: Finding the Greatest Common Factor (GCF)
Simplifying a fraction means expressing it in its lowest terms. This involves finding the greatest common factor (GCF) of the numerator and the denominator and dividing both by that factor. The GCF is the largest number that divides both the numerator and the denominator without leaving a remainder.
Let's find the GCF of 6 and 8:
The factors of 6 are 1, 2, 3, and 6. The factors of 8 are 1, 2, 4, and 8.
The common factors of 6 and 8 are 1 and 2. The greatest common factor is 2.
Simplifying 6/8 to its Lowest Terms
Now that we've found the GCF (2), we can simplify 6/8 by dividing both the numerator and the denominator by 2:
6 ÷ 2 = 3 8 ÷ 2 = 4
Therefore, the simplified fraction is 3/4. This means that 6/8 and 3/4 represent the same portion of a whole; they are equivalent fractions.
Visual Representation of Equivalent Fractions
Imagine a pizza cut into 8 equal slices. If you eat 6 slices, you've eaten 6/8 of the pizza. Now imagine the same pizza, but this time it's cut into only 4 equal slices. If you eat 3 of those slices, you've still eaten the same amount of pizza – 3/4. This visual representation clearly demonstrates the equivalence of 6/8 and 3/4.
Methods for Finding Equivalent Fractions
There are several ways to find equivalent fractions:
-
Dividing by the GCF: As demonstrated above, this is the most efficient method for simplifying fractions to their lowest terms.
-
Multiplying by a Common Factor: You can create equivalent fractions by multiplying both the numerator and the denominator by the same number (other than zero). For example, multiplying both the numerator and denominator of 3/4 by 2 gives you 6/8, demonstrating that 3/4 and 6/8 are equivalent. Multiplying by 3 would give 9/12, another equivalent fraction.
-
Using a visual representation: Drawing diagrams or using manipulatives can help visualize the relationship between equivalent fractions.
Practical Applications of Fraction Equivalence
Understanding fraction equivalence is vital in various real-world situations and mathematical contexts:
-
Measurement: Converting between different units of measurement often involves working with equivalent fractions. For instance, converting inches to feet requires understanding the relationship between these units.
-
Baking and Cooking: Recipes often require fractions, and understanding equivalent fractions allows for adjustments based on the number of servings.
-
Percentage Calculations: Percentages are essentially fractions with a denominator of 100. Understanding fraction equivalence is crucial for converting between fractions and percentages.
-
Algebra and Higher Mathematics: Fraction equivalence forms the foundation for many algebraic manipulations and more advanced mathematical concepts.
Beyond 6/8: Exploring Other Examples
Let's extend our understanding by exploring the simplification of other fractions:
-
12/16: The GCF of 12 and 16 is 4. Dividing both by 4 gives 3/4. Therefore, 12/16 is equivalent to 3/4.
-
18/24: The GCF of 18 and 24 is 6. Dividing both by 6 gives 3/4. Again, we see that 18/24 is equivalent to 3/4.
-
24/32: The GCF of 24 and 32 is 8. Dividing both by 8 gives 3/4. This further reinforces the concept that many fractions can be simplified to the same equivalent form.
Improper Fractions and Mixed Numbers
When the numerator is larger than the denominator, we have an improper fraction. Improper fractions can be converted into mixed numbers, which consist of a whole number and a proper fraction. For instance, if we had the fraction 11/4, this is an improper fraction because the numerator (11) is greater than the denominator (4). To convert it to a mixed number, we divide the numerator by the denominator: 11 ÷ 4 = 2 with a remainder of 3. Therefore, 11/4 is equivalent to 2 3/4 (two and three-quarters). Understanding improper fractions and their conversion to mixed numbers is another essential aspect of working with fractions.
Conclusion: The Importance of Understanding Fraction Equivalence
The seemingly simple question of what fraction is equal to 6/8 leads to a rich exploration of fraction equivalence and its numerous applications. Understanding how to simplify fractions to their lowest terms is a fundamental skill in mathematics, essential for problem-solving and further mathematical studies. The principles discussed in this article—finding the greatest common factor, understanding equivalent fractions through multiplication and division, and working with improper fractions and mixed numbers—are crucial for mastering fractions and building a strong foundation in mathematics. The ability to confidently work with fractions is essential for success in various academic and real-world scenarios. From understanding recipes to solving complex equations, the understanding of equivalent fractions is an invaluable tool.
Latest Posts
Latest Posts
-
How Many Glass Is 1 Liter Of Water
Jul 22, 2025
-
How Many Ounces Is 4 Cups Of Green Beans
Jul 22, 2025
Related Post
Thank you for visiting our website which covers about What Fraction Is Equal To 6 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.