What Is 0.02 As A Percent
Kalali
Apr 28, 2025 · 5 min read
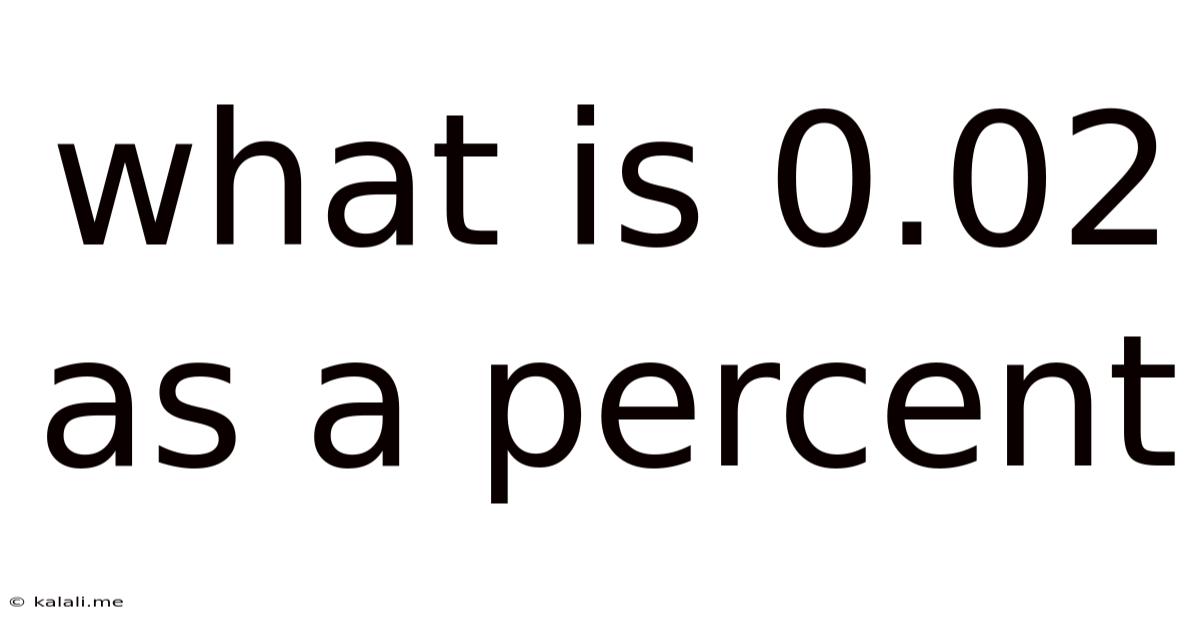
Table of Contents
What is 0.02 as a Percent? A Comprehensive Guide to Decimal-to-Percentage Conversions
Understanding decimal-to-percentage conversions is a fundamental skill in various fields, from finance and statistics to everyday calculations. This comprehensive guide will explore the question, "What is 0.02 as a percent?", providing a clear and detailed explanation of the process. We'll delve into the underlying principles, offer practical examples, and discuss common applications of this conversion. This guide will also explore related concepts, equipping you with a solid understanding of decimal and percentage representations.
Meta Description: Learn how to convert decimals to percentages. This comprehensive guide explains what 0.02 is as a percent and explores the underlying principles of decimal-to-percentage conversions, offering practical examples and real-world applications.
Understanding Decimals and Percentages
Before we tackle the specific conversion of 0.02, let's briefly review the concepts of decimals and percentages.
-
Decimals: Decimals represent fractions where the denominator is a power of 10 (10, 100, 1000, etc.). The decimal point separates the whole number part from the fractional part. For instance, 0.02 signifies two hundredths (2/100).
-
Percentages: Percentages represent fractions where the denominator is always 100. The "%" symbol indicates that a number is expressed as a fraction of 100. For example, 2% means 2 out of 100, or 2/100.
Converting Decimals to Percentages: The Core Principle
The core principle behind converting a decimal to a percentage is to multiply the decimal by 100. This is because percentages are essentially decimals expressed as parts of 100. The multiplication by 100 shifts the decimal point two places to the right.
Calculating 0.02 as a Percentage
Applying this principle to our question, "What is 0.02 as a percent?", we simply multiply 0.02 by 100:
0.02 * 100 = 2
Therefore, 0.02 is equal to 2%.
Practical Applications: Real-World Examples
Understanding decimal-to-percentage conversions is crucial in various everyday situations and professional contexts. Let's explore some practical examples:
1. Finance:
- Interest Rates: Banks often express interest rates as decimals. If a bank offers a savings account with an interest rate of 0.02, it means a 2% annual interest rate. This is vital for calculating the interest earned on your savings.
- Investment Returns: Investment returns are often represented as decimals. A return of 0.05 on an investment translates to a 5% return. Understanding this conversion is crucial for evaluating investment performance.
- Discounts: Sales discounts are frequently expressed as percentages. A 0.02 discount on an item means a 2% discount.
2. Statistics and Data Analysis:
- Probabilities: Probabilities are often expressed as decimals. A probability of 0.02 indicates a 2% chance of an event occurring.
- Data Representation: Data representation often involves converting decimals into percentages for easier understanding and visualization in charts and graphs. For example, representing market share or survey results.
3. Everyday Life:
- Tip Calculations: Calculating tips often involves using percentages. If you want to leave a 2% tip, you would multiply the bill amount by 0.02 (or 0.02 expressed as 2%).
- Sales Tax: Sales taxes are also expressed as percentages. Understanding decimal-to-percentage conversions helps calculate the total cost including sales tax.
Beyond 0.02: Generalizing the Conversion Process
The process of converting decimals to percentages remains consistent regardless of the decimal value. Here's a generalized approach:
- Multiply the decimal by 100.
- Add the "%" symbol to indicate a percentage.
Let's look at some further examples:
- 0.5 = 0.5 * 100 = 50%
- 0.15 = 0.15 * 100 = 15%
- 0.75 = 0.75 * 100 = 75%
- 1.25 = 1.25 * 100 = 125% (Note: Percentages can be greater than 100%)
Converting Percentages to Decimals: The Reverse Process
It's equally important to understand the reverse process—converting percentages back to decimals. To do this, you divide the percentage by 100. This shifts the decimal point two places to the left.
For example:
- 50% = 50 / 100 = 0.5
- 15% = 15 / 100 = 0.15
- 2% = 2 / 100 = 0.02
Understanding Decimal Places and Precision
When dealing with decimals and percentages, it's crucial to consider the number of decimal places for accuracy and precision. In some contexts, rounding to a specific number of decimal places might be necessary. For example, when dealing with financial calculations, rounding to two decimal places (representing cents) is standard practice.
Advanced Applications: Compound Interest and Growth Rates
Decimal-to-percentage conversions play a vital role in more complex financial calculations such as compound interest and growth rates. Compound interest, where interest is calculated on both the principal amount and accumulated interest, utilizes decimal representations of interest rates to calculate future values. Similarly, growth rates in various fields (economics, biology, etc.) often employ decimal representations that are then converted into percentages for easier interpretation.
Troubleshooting Common Mistakes
While the conversion process is straightforward, some common mistakes can occur:
- Forgetting to multiply by 100: Remember that the crucial step is to multiply the decimal by 100 to obtain the percentage.
- Incorrect placement of the decimal point: Ensure the decimal point is moved correctly two places to the right when multiplying by 100.
- Misinterpreting percentages greater than 100%: Percentages can exceed 100%, representing values greater than the whole.
Conclusion: Mastering Decimal-to-Percentage Conversions
Mastering the conversion between decimals and percentages is a valuable skill applicable across numerous disciplines. This guide has explored the core principles, provided practical examples, and discussed advanced applications of this fundamental mathematical concept. By understanding these principles and practicing the conversion process, you will be equipped to confidently handle decimal-to-percentage conversions in various real-world scenarios. Remember the key: multiply by 100 to go from decimal to percent, and divide by 100 to go from percent to decimal. This simple yet powerful technique will enhance your numerical literacy and problem-solving abilities significantly.
Latest Posts
Latest Posts
-
Cuales Son Los Centimetros En Un Metro
Apr 28, 2025
-
How Much Is 170 Cm In Inches
Apr 28, 2025
-
What Was Darwin Influences On Lyell And Hutton
Apr 28, 2025
-
Convert 99 Degrees Fahrenheit To Celsius
Apr 28, 2025
-
How Many Grams Is 25 Milligrams
Apr 28, 2025
Related Post
Thank you for visiting our website which covers about What Is 0.02 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.